在做特征选择时,可能面临两个问题:特征与类别预测有多大相关性,特征之间有多大冗余度。在特征选择中,“最好的m个特征不一定是m个最好的特征”,从相关度与冗余度来看,最好的m个特征是指与分类最相关的特征,但由于最好的m个特征之间可能存在冗余,因此最相关的m个特征并不一定比其他m个特征产生更好的分类准确率。可以看出,特征选择可以分为两个过程:1、怎样度量特征相关性。2、怎样解决特征之间的冗余。
互信息
互信息可以度量两个变量x,y之间的相关关系。如下图所示:
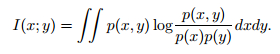
考虑特征x与分类目标c,计算I(x,c),I(x,c)的大小代表了x与c之间的关联度的大小。从所有特征中选出与c之间互信息最大的m个特征,就可以得到与c最相关的m个特征。
最大相关度与最小冗余度
设S表示特征{xi}的集合,|S|=m. 为了选出m个最相关特征,使得S满足如下公式:
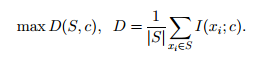
可见目标是选出m个平均互信息最大的集合S。
S很可能包含相关度很大的特征,也就是说特征之间存在冗余。集合S的冗余度如下式所示:
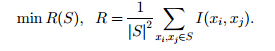
最终目标是求出拥有最大相关度-最小冗余度的集合S,直接优化下式:
直观上说D的增大,R的减小都会使得目标函数增大。
假设现在S中已有m-1个特征,现在需要从余下的特征中选择第m个特征。
特征选择过程
特征选择的目的是选择出一个具有很好分类效果的精简特征集。为了达到此目的,可以分两步进行:第一步,利用mrmr选出候选特征集;第二步,利用其它方法选出精简特征集。
主要步骤:
- 将数据进行处理转换的过程(注:为了计算两个特征的联合分布和边缘分布,需要将数据归一化到[0,255]之间,并且将每一维特征使用合理的数据结构进行存储)
- 计算特征之间、特征与响应变量之间的分布及互信息
- 对特征进行mrmr得分,并进行排序




大佬有没有代码呀
你好,可以参考互信息计算代码:https://www.omegaxyz.com/2020/12/18/mine/
The minimal correlation minimum (MCRR) algorithm is very attractive, Thank you for sharing this great article.
thank you i am student ,could i ask you some questions?
Sure.