基于拥挤距离与变异支配的多目标PSO算法

这一篇是Xue Bing在一区cybernetics发的论文，里面提出了两个多目标PSO特征选择算法，一个是NSPSO另一个是CMDPSO。其中NSPSO是参考了NSGA2的框架和思想。下面具体说说CMDPSO。

CMDPSO全称是Crowding，Mutation，Dominance PSO算法。

NSPSO算法概述与实现

基于非支配排序的多目标PSO算法

基于非支配排序的多目标PSO算法MATLAB实现

PSO算法

MATLAB粒子群优化算法实现（PSO）

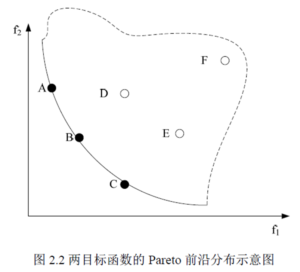
个体拥挤距离

在同一层Fk中需要进行选择性排序，按照个体拥挤距离(crowding distance)大小排序。个体拥挤距离是Fk上与i相邻的个体i+1和i-1之间的距离，其计算步骤为：
①对同层的个体距离初始化，令L[i]d=0（表示任意个体i的拥挤距离）。
②对同层的个体按照第m个目标函数值升序排列。
③对于处在排序边缘上的个体要给予其选择优势。
④对于排序中间的个体，求拥挤距离：

（其中：L[i+1]m为第i+1个体的第m目标函数值fmax，fmin分别为集合中第m目标函数的最大和最小值。）
⑤对于不同的目标函数，重复②到④的步骤，得到个体i的拥挤距离L[i]d，有限选择拥挤距离较大的个体，可以是计算结果在目标空间均匀地分布，维持群体的多样性。

伪代码

注意archive中存的是每一代的精英粒子集合

具体流程

• ①划分数据集
• ②初始化精英集合和存档Archive
• ③计算拥挤距离
• ④二进制锦标赛选择一个一个精英个体来作为gbest指导更新
• ⑤更新粒子
• ⑥使用变异算子
• ⑦粒子真实评价
• ⑧将LeaderSet加入存档
• ⑨迭代完成后计算存档中的两个目标值