最大信息系数 maximal information coefficient (MIC),又称最大互信息系数
目的:Maximal Information Coefficient (MIC) 最大信息系数,属于Maximal Information-based Nonparametric Exploration (MINE) 最大的基于信息的非参数性探索,用于衡量两个变量X和Y的线性或非线性的强度。
MIC度量具有普适性。其不仅可以发现变量间的线性函数关系,还能发现非线性函数关系(指数的,周期的);不仅能发现函数关系,还能发现非函数关系(比如函数关系的叠加,或者有趣的图形模式)。
MIC度量具有均衡性。对于相同噪声水平的函数关系或者非函数关系,MIC度量具有近似的值。所以MIC度量不仅可以用来纵向比较同一相关关系的强度,还可以用来横向比较不同关系的强度。
优点:generality:拥有足够的统计样本时,可以捕获广泛的关系,而不限定于特定的函数类型(如线性、指数型、周期型等)。
equitability:对不同类型的噪声程度同等的关系给予相近的分数。
缺点:“MIC的统计能力遭到了一些质疑,当零假设不成立时,MIC的统计就会受到影响。在有的数据集上不存在这个问题,但有的数据集上就存在这个问题。”
最早出处:http://science.sciencemag.org/content/334/6062/1518.full
MIC度量计算的方法。具有两个属性的数据点的集合分布在两维的空间中,使用m乘以n的网格划分数据空间,使落在第(x,y)格子中的数据点的频率作为P(x,y)的估计即![]() ,使落在第x行的数据点的频率作为P(x)的估计,同理获得P(y)的估计。然后计算随机变量X、Y的互信息。因为m乘以n的网格划分数据点的方式不止一种,所以我们要获得使互信息最大的网格划分。然后使用归一化因子,将互信息的值转化为(0,1)区间之内。最后,找到能使归一化互信息最大的网格分辨率,作为MIC的度量值。其中网格的分辨率限制为m x n < B,
,使落在第x行的数据点的频率作为P(x)的估计,同理获得P(y)的估计。然后计算随机变量X、Y的互信息。因为m乘以n的网格划分数据点的方式不止一种,所以我们要获得使互信息最大的网格划分。然后使用归一化因子,将互信息的值转化为(0,1)区间之内。最后,找到能使归一化互信息最大的网格分辨率,作为MIC的度量值。其中网格的分辨率限制为m x n < B,![]() 。将MIC的计算过程概括为公式为:
。将MIC的计算过程概括为公式为: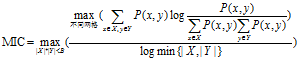
详解:
详细解释来源:http://blog.csdn.net/u014271612/article/details/51781250
MIC计算分为三个步骤:
1.给定i、j,对XY构成的散点图进行i列j行网格化,并求出最大的互信息值
2.对最大的互信息值进行归一化
3.选择不同尺度下互信息的最大值作为MIC值

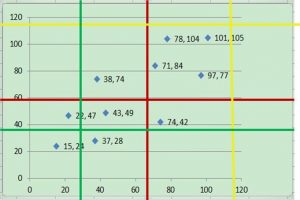
(1)红色网格化方案将所有数据点分为四个区域:左上,右上,左下,右下。每个区域对应的数据点数量为1,4,4,1。将数据点数归一化得到四个区域的数据点频率,分别为0.1,0.4,0.4,0.1。也就是说,此时,X有两种取值:左和右,Y有两种取值:上和下。P(X=左,Y=上)=0.1,P(X=右,Y=上)=0.4,P(X=左,Y=下)=0.4,P(X=右,Y=下)=0.1。并且,P(X=左)=0.5,P(X=右)=0.5,P(Y=上)=0.5,P(Y=下)=0.5。

(2)对最大的互信息值进行归一化
将得到的最大互信息除以log(min(X,Y)),即为归一化!
(3)选择不同尺度下互信息的最大值作为MIC值
上面讲述了给定i和j的情况下M(X,Y,D,i,j)的计算方法。这一步就是给定很多(i,j)值,计算每一种情况下M(X,Y,D,i,j)的值,将所有M(X,Y,D,i,j)中的最大那个值作为MIC值。注意的是,这里的(i,j)是有条件的,要满足,n表示数据集D的数据量。当然,B(n)这个值可以自己定,这里是别人做实验认为效果最好的值。
参考资料:
http://blog.csdn.net/lijiancheng0614/article/details/50826270
http://blog.csdn.net/u014271612/article/details/51781250


MIC的缺点从哪篇文章里看到的?
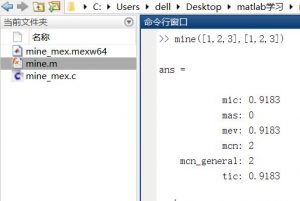
有matlab代码吗?
https://www.omegaxyz.com/2018/08/03/mifs/