文章目录
关键词:高维特征选择,马尔科夫毯,变邻域搜索算法,特征分组
期刊:Information Science (一区)

①马尔科夫毯:

把一个随机变量全集U分成互斥的三部分,变量X以及集合A和B,三个子集没有交集,并集即为全集U;如果说给定集合A时,变量X与集合B没有任何关系,则称集合A为变量X的马尔可夫毯。在式(2-16)中,集合MB即为我说的集合A,{U-MB-{X}}即为我说的集合B,符号“⊥”表示“独立”,符号“|”表示在给定xx条件下,因此可读为“在给定集合MB时,变量X与{U-MB-{X}}独立”。
打个比方说,全集U是整个社会,X是你个人,MB就是你生活圈子里的人。按照哲学的说法,万事万物都是有联系的;但是,你并不会与社会里的所有人有什么关系,而是通过你的生活圈子和他们有间接的关系,即当给定你的生活圈子以后,你和社会其余的人是没啥关系的(独立的)。
②对称不确定性 (Symmetrical Uncertainty)
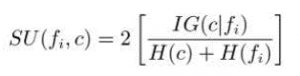
对每一个特征fi , 计算其对称不确定性,其中, IG(c l fi)表示类别c 与特征Ji 之间的信息增益, H(c)和H(fi) 分别表示类别c与特征Fi 的信息熵(entropy) 给定一个阔值γ, 如SU(fi,c) ≥γ,则fi对于类别c 来说是强相关特征,应该被保留,反之fi应该被去除。
③近似马尔科夫毯(Approximate Markov Blankets)
对于两个特征Xi和Xj(i≠j),Xj是Xi的近似马尔科夫毯的条件为:SU(Xj,c)>=SU(Xi,c),
且SU(Xi,Xj)≥SU(Xi,c)
一个特征Xi 为主元素,当且仅当没有元素是Xi 的近似马尔科夫毯。
④主元素组(Predominant group)生成算法——GPGG

STEP1:冗余性分析. 对每一个特征Xi , 根据其对称不确定性给定一个阈值α, 如SU(Xi,y) > α ,则且
对于类别y来说是强相关特征,放入集合L中。
STEP2:根据SU的值进行降序排序。
STEP3:利用近似马尔科夫毯方法(判断每个元素是否存在马尔科夫毯)从L中寻找主元素放到集合g中。
⑤变邻域搜索算法(Variable Neighborhood Search,VNS)
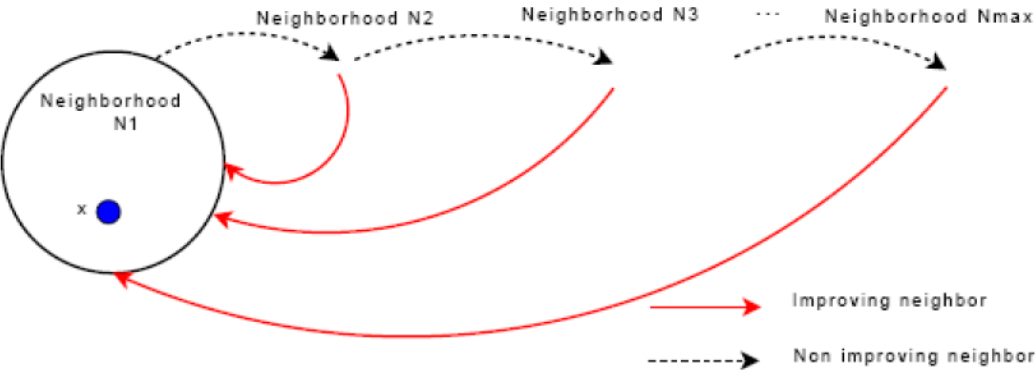
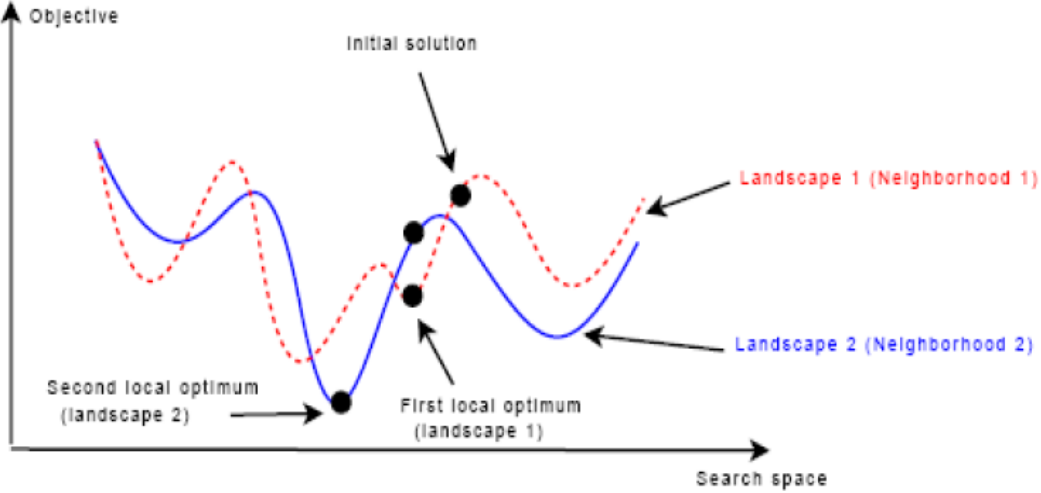
变邻域搜索算法的主要思想是:采用多个不同的邻域进行系统搜索。首先采用最小的邻域搜索,当无法改进解时,则切换到稍大一点的邻域。如果能继续改进解,则退回到最小的邻域,否则继续切换到更大的邻域。

⑥PGVNS算法(PredominantGroupbasedVariableNeighborhoodSearch)

为了将VNS算法应用到高维数据集上,作者提出了基于VNS主元素组的特征选择方法,
首先利用GPGG算法产生主元素组作为初始的解,再 利用shaking method选出新的解集,如此迭代最终获得最好的解集。
原文:García-Torres M, Gómez-Vela F, Melián-Batista B, et al. High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach[J]. Information Sciences, 2016, 326(C):102-118.




