文章目录
知识图谱嵌入
融合事实信息的知识图谱嵌入
步骤：
语义匹配模型
语义匹配模型利用基于相似性的评分函数。它们通过匹配实体的潜在语义和向量空间表示中包含的关系来度量事实的可信性。
RESCAL模型及其变体
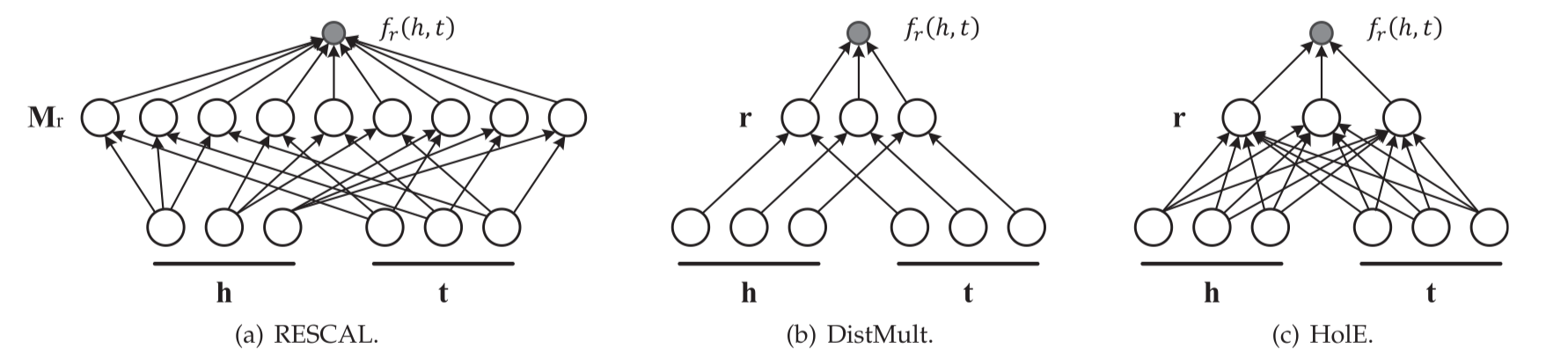
RESCAL模型（双线性模型）
实体用向量表示，关系用矩阵表示。该关系矩阵对潜在因素之间的成对交互作用进行了建模。评分函数是一个双线性函数。
![f_{r}(h, t)=\mathbf{h}^{\top} \mathbf{M}_{r} \mathbf{t}=\sum_{i=0}^{d-1} \sum_{j=0}^{d-1}\left[\mathbf{M}_{r}\right]_{i j} \cdot[\mathbf{h}]_{i} \cdot[\mathbf{t}]_{j}](https://www.omegaxyz.com/wp-content/ql-cache/quicklatex.com-98bfddc86495b40a66a7e359de361df8_l3.svg "Rendered by QuickLaTeX.com")
DistMult模型：将关系矩阵简化为对角矩阵
缺点：过于简化，只能处理对称的关系，这显然对于一般的KGs是不能完全适用的。
HolE(Holographic Embeddings)
HolE 将 RESCAL 的表达能力与 DistMult 的效率和简单性相结合。使用循环相关操作（circular correlation operation）
ComplEx(Complex Embeddings)
引入复数扩展DistMult，以便更好地对非对称关系进行建模，此时，实体、关系都在复数空间，非对称关系的事实可以根据涉及实体的顺序得到不同的分数。每个 ComplEx 都有一个等价的 HolE，同时，如果在嵌入上施加共轭对称，那么，HolE是ComplEx的特殊情况。
ANALOGY模型
ANALOGY 扩展了 RESCAL，从而进一步对实体和关系的类比属性进行建模。尽管 ANALOGY 表示关系为矩阵，这些矩阵可以同时对角化成一组稀疏的准对角矩阵。结果表明，前面介绍的 DistMult、HolE、ComplEx 等方法都可以归为 ANALOGY 的特例。
基于神经网络的匹配
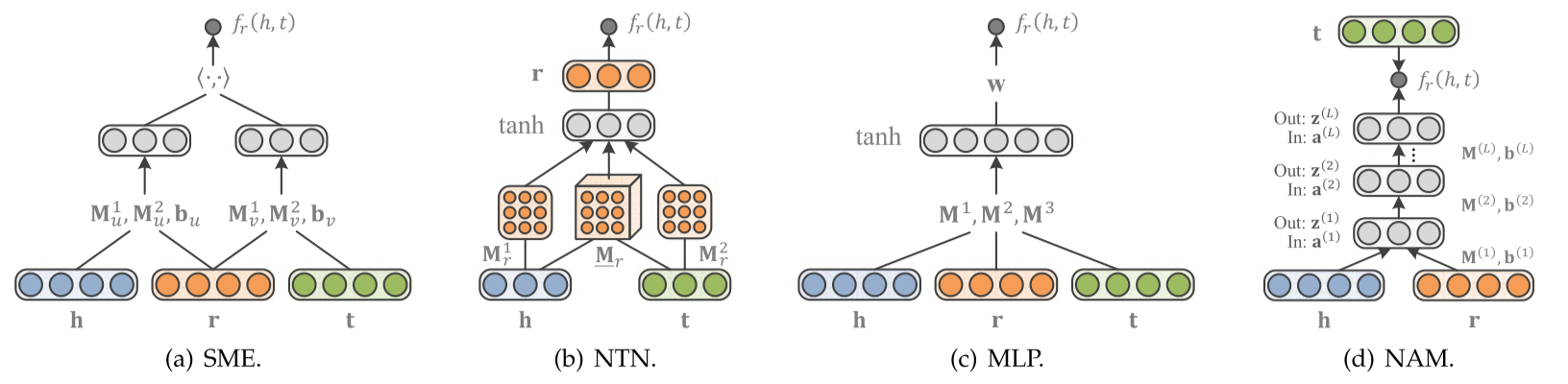
语义匹配能量模型 (SME)
首先将实体和关系投影到输入层中的嵌入向量，然后关系r与头尾实体分别组合至隐藏层。输出则是评分函数。SME 有两个版本：线性版本和双线性版本。
神经张量网络模型 (NTN)
给定一个事实，它首先将实体投影到输入层中的嵌入向量。然后，将这两个实体 h,t 由关系特有的关系张量(以及其他参数) 组合，并映射到一个非线性隐藏层。最后，一个特定于关系的线性输出层给出了评分。NTN是迄今为止最具表达能力的模型，但是参数过多，处理大型知识图谱效率较差。
多层感知机 (MLP)
MLP 是一种更简单的方法，在这种方法中，每个关系 (以及实体) 都是由一个向量组合而成的。给定一个事实，将嵌入向量 h、r 和 t 连接在输入层中，并映射到非线性的隐藏层。然后由线性输出层生成分数。
神经关联模型 (NAM)
给定一个事实，它首先将头实体的嵌入向量和输入层中的关系连接起来，在“deep”神经网络隐藏层的前馈过程之后，通过匹配最后一个隐藏层的输出和尾实体的嵌入向量来给出分数。
语义匹配模型总结
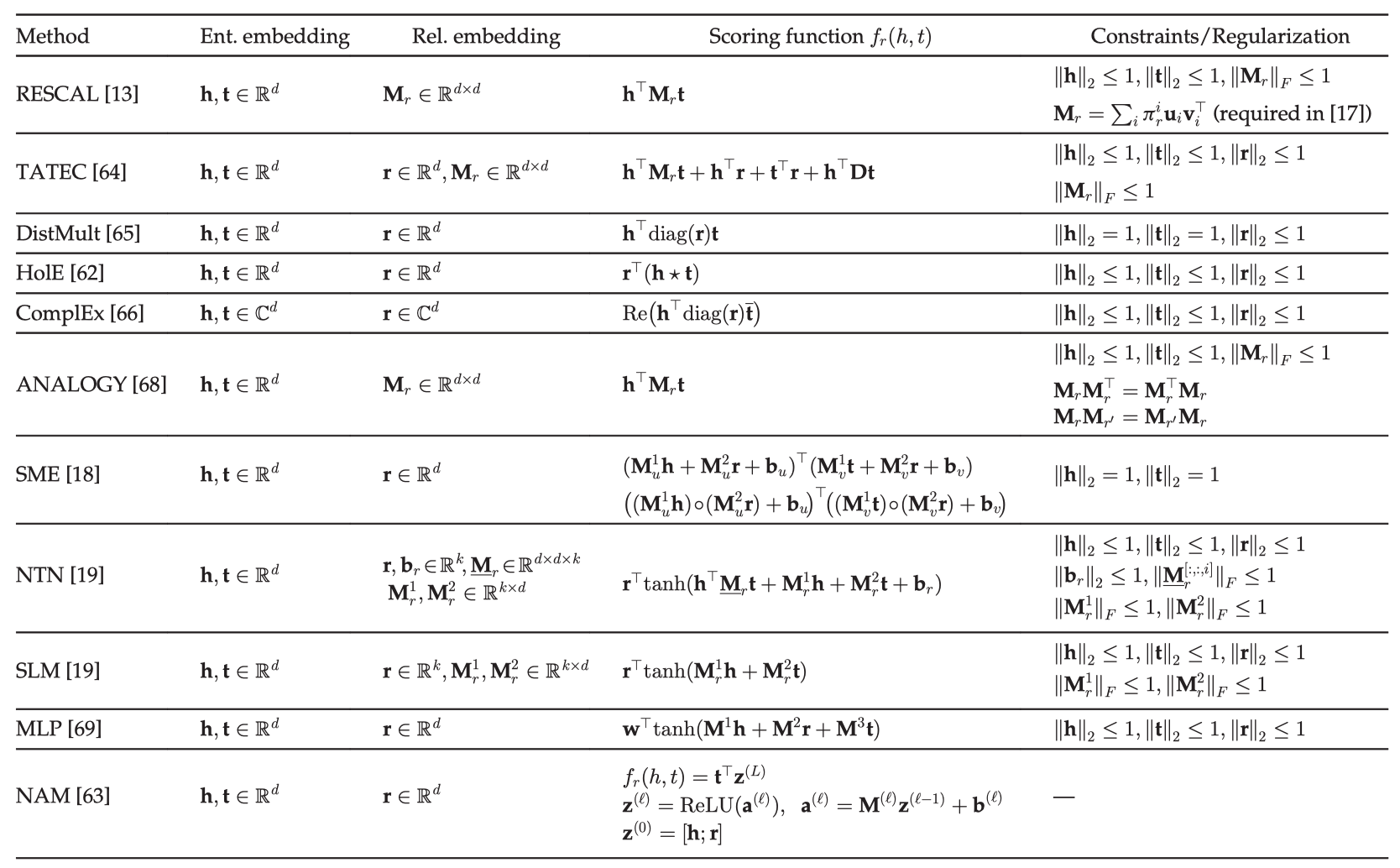
参考文献：Wang Q , Mao Z , Wang B , et al. Knowledge Graph Embedding: A Survey of Approaches and Applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, PP(99):1-1.
