知识图谱嵌入
知识图谱(KG)是由实体 (节点) 和关系 (不同类型的边) 组成的多关系图。每条边都表示为形式 (头实体、关系、尾实体) 的三个部分,也称为事实,表示两个实体通过特定的关系连接在一起。虽然在表示结构化数据方面很有效,但是这类三元组的底层符号特性通常使 KGs 很难操作。为了解决这个问题,提出了一种新的研究方向——知识图谱嵌入。关键思想是嵌入 KG 的组件,包括将实体和关系转化为连续的向量空间,从而简化操作,同时保留 KG 的原有的结构。那些实体和关系嵌入能进一步应用于各种任务中,如 KG 补全、关系提取、实体分类和实体解析。
融合事实信息的知识图谱嵌入
步骤:
①使用连续向量空间表示实体关系,关系通常被视为向量空间的运算。
②定义评分函数,用来测量事实的合理性。
③学习实体关系的表示,优化问题:最大化全局观测事实的合理性。
有两个主要分类:
①平移距离模型 translational distance models 前者使用基于距离的评分函数
②语义匹配模型 semantic matching models 后者使用基于相似度的评分函数
平移距离模型
平移距离模型利用基于距离的评分函数。通常是在通过关系进行翻译之后,用两个实体之间的距离来衡量一个事实的合理性。下图是TransE及其变体的详细解释。
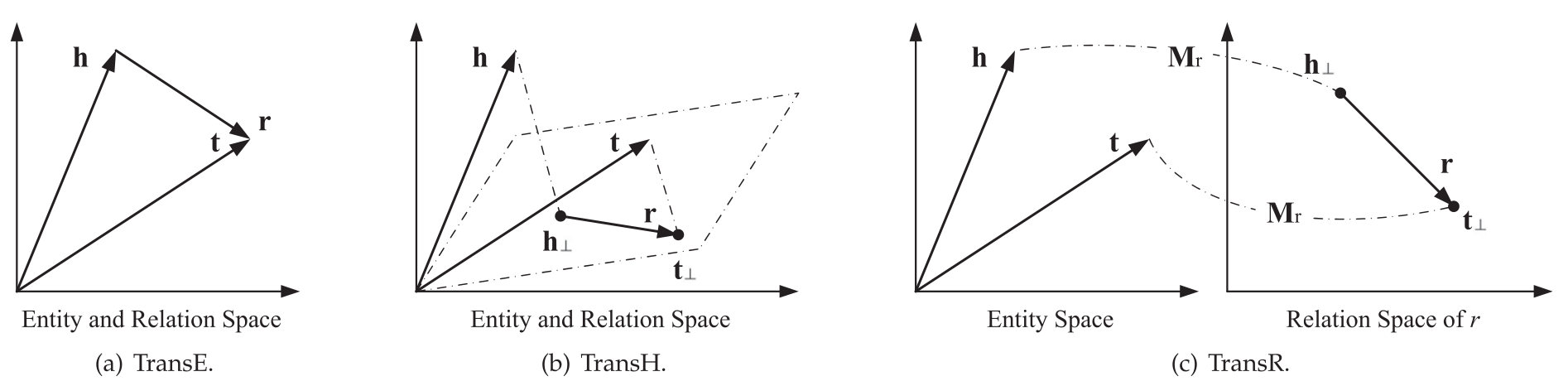
TransE及其变体
TransE:最具代表性的知识图谱嵌入
实体和关系都在同一空间,对于每一个三元组(h,r,t)TransE 希望:
评分函数为:
缺点:复杂关系例如,一对多 、 多对一 、多对多关系不适用。
TransH:解决TransE在多元关系上的缺陷
可以让一个实体在不同的关系下拥有不同的表示,方法对于一个三元组 (h, r, t) , TransH 首先将头实体向量 h 和尾实体向量 r,沿法线 wr,投影到关系 r 对应的超平面上,用 h⊥和 t⊥表示如下:
TransR:实体和关系在不同的语义空间中
每一个关系关联着一个特定的空间,首先需要将实体映射到关系空间。
其中转换方式是一个从实体空间到关系空间的投影矩阵。
缺点:转换方式是空间投影,复杂度高。
TransD:对TransR的简化
将TransR的投影矩阵分解为两个向量的积。
TransSparse:在投影矩阵上强化稀疏性来简化TransR
它有两种版本,一个是共享型,另一个是独立型,其中share版本的头尾实体共享头一个稀疏投影矩阵,独立型的头尾实体则分别有一个投影矩阵。
TransM:放松TransE的转化要求,提高模型性能
为每个事实分配特定的关系权重θ,改变评分函数。
通过对一对多、多对一和多对多分配较小的权重,TransM 模型使得 t 在上述的复杂关系中离 h+r 更远。
ManifoldE
把 t 近似地位于流形体上,即一个以 h+r 为中心半径为 theta_r 的超球体。
TransF
只需要 t 与 h+r 位于同一个方向,同时 h 与 t-r 也位于同一个方向。
TransA
为每个关系 r 引入一个对称的非负矩阵 Mr,并使用自适应马氏距离定义评分函数。
高斯嵌入:考虑到实体与关系的不确定性,使用随机变量建模
KG2E:使用高斯分布来表示实体和关系
其中高斯分布的均值表示的是实体或关系在语义空间中的中心位置,而高斯分布的协方差则表示该实体或关系的不确定度。KG2E 模型将实体和关系表示为从多变量高斯分布中抽取的随机向量。
通过测量 t-h 和 r 这两个随机向量之间的距离来为一个事实评分,通过 两种方法来进行测量。一种是通过 KL 散度(KL 距离)来进行测量,另一种是计算概率的内积。
TransG
实体采用高斯分布,但它认为关系具有多重语义,需要采用混合的高斯分布的表示
其他距离模型
非结构化模型UM(Unstructured model)
TransE的简单版本,直接设置所有的r=0
结构化嵌入SE(Structured embedding)
通过使用两个独立的矩阵 为每个关系 r 对头尾实体进行投影
平移距离模型总结
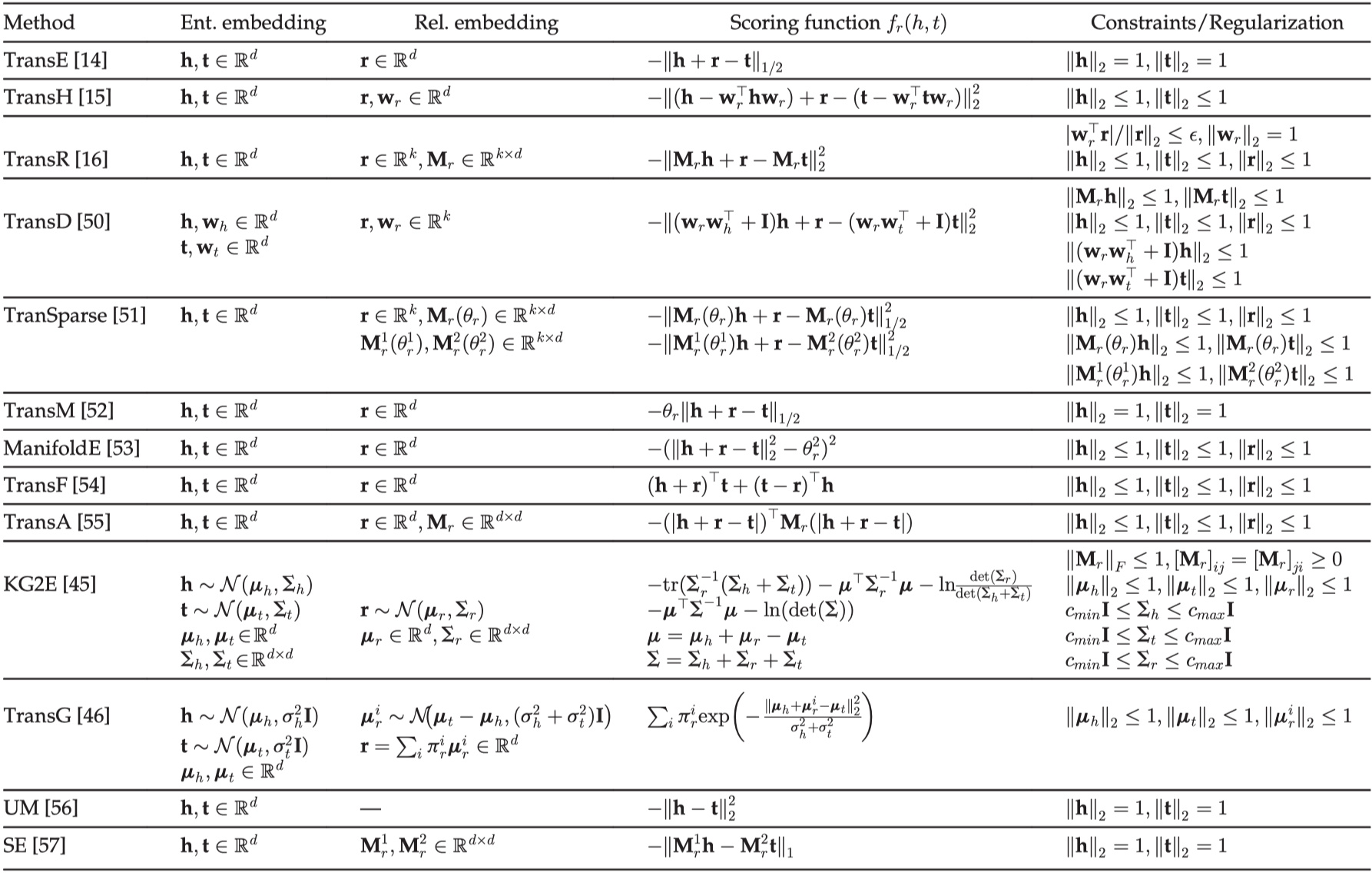
参考文献:Wang Q , Mao Z , Wang B , et al. Knowledge Graph Embedding: A Survey of Approaches and Applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, PP(99):1-1.