参数估计(parameter estimation)
统计推断的一种。根据从总体中抽取的随机样本来估计总体分布中未知参数的过程。从估计形式看,区分为点估计与区间估计:从构造估计量的方法讲,有矩法估计、最小二乘估计、似然估计、贝叶斯估计等。
参数估计的目的
利用样本的已知信息,反推样本的具体环境,即反推参数值。
举例来说,一堆离散的样本点,需要拟合,拟合出的函数的w系数,即是反推的参数值。
这点便是机器学习方法中的精髓。
极大似然估计的的方法
利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
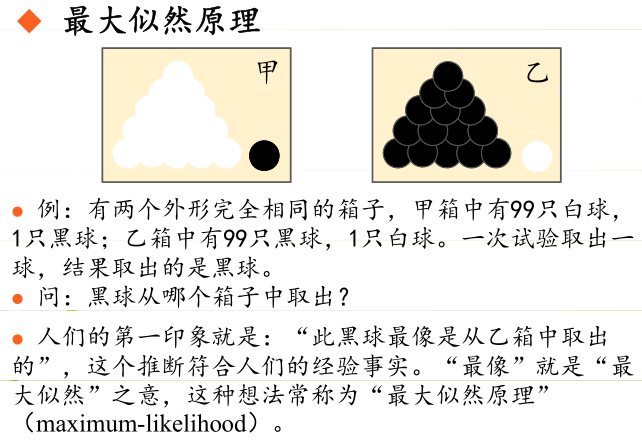
极大似然原理最简单的理解就是:样本所展现的状态便是所有可能状态中出现概率最大的状态。
即在样本x条件下,对参数theta的估计
多数情况下我们是根据已知条件来推算结果,而极大似然估计是已经知道了结果,然后寻求使该结果出现的可能性最大的条件,以此作为估计值。
举例来说,小明长得像A,长得不像B,因此我们在现有的条件下,可以推断小明与A有血缘关系,这便是极大似然估计的一个粗暴理解。
在机器学习中,极大似然估计便是经验风险最小化的一个例子。当模型是条件概率分布式且损失函数是对数损失函数是,经验风险最小化就等价于极大似然估计;同样的,极大似然估计也是逻辑回归(logistic regression)的本质。