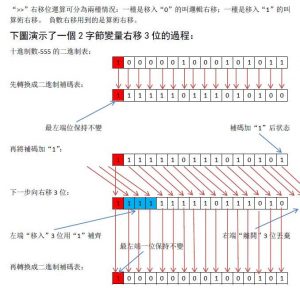
简介
红黑树的性质
- 性质1. 节点是红色或黑色。
- 性质2. 根节点是黑色。
- 性质3 每个叶节点(NIL节点,空节点)是黑色的。
- 性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
PAT1135 Is It A Red-Black Tree
There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:
- (1) Every node is either red or black.
- (2) The root is black.
- (3) Every leaf (NULL) is black.
- (4) If a node is red, then both its children are black.
- (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.
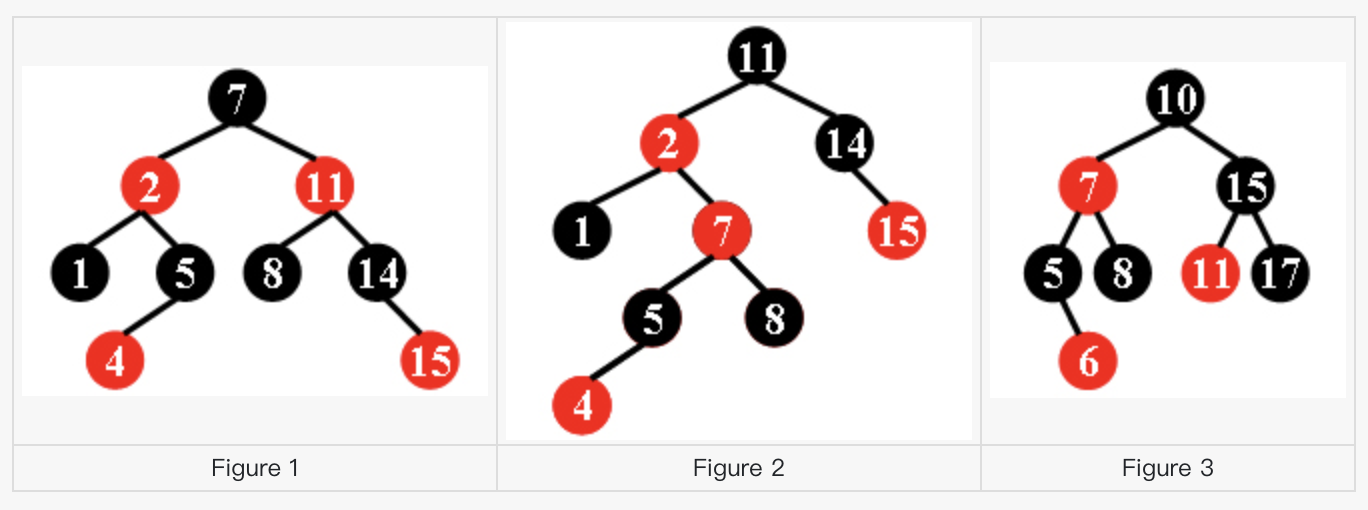
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.
Input Specification:
Each input file contains several test cases. The first line gives a positive integer K (30) which is the total number of cases. For each case, the first line gives a positive integer N (30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.
Output Specification:
For each test case, print in a line “Yes” if the given tree is a red-black tree, or “No” if not.
Sample Input:
|
1 2 3 4 5 6 7 8 |
3 9 7 -2 1 5 -4 -11 8 14 -15 9 11 -2 1 -7 5 -4 8 14 -15 8 10 -7 5 -6 8 15 -11 17 |
Sample Output:
|
1 2 3 4 |
Yes No No |
C++代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include<iostream> #include<vector> #include<cmath> using namespace std; vector<int> arr; struct node{ int val; struct node *left, *right;//以链表的方式存储 }; node* build(node *root, int v){ //递归二叉查找树 if(root == NULL){ root = new node(); root->val = v; root->left = root->right = NULL; }else if(abs(v) <= abs(root->val))//小于根节点的为左边递归 root->left = build(root->left, v); else root->right = build(root->right, v); return root; } bool judgeBlackChild(node *root){ //判断红色节点的孩子为黑色 if(root == NULL)return true; if(root->val < 0){//red negative if(root->left != NULL && root->left->val < 0 )return false; if(root->right != NULL && root->right->val < 0)return false; } return judgeBlackChild(root->left) && judgeBlackChild(root->right); } int getNum(node *root){ if(root == NULL)return 0; int l = getNum(root->left); int r = getNum(root->right); return root->val > 0 ? max(l, r) + 1 : max(l, r); //大于0是黑色节点,如果是黑色节点则加1,否则不变 } int judgeBlackNum(node *root){ //判断数量是否相同 if(root == NULL)return true; int l = getNum(root->left); int r = getNum(root->right); if(l != r)return false; return judgeBlackNum(root->left) && judgeBlackNum(root->right); } int main(){ int k, n; cin>>k; for(int i = 0; i < k; i++){ cin>>n; arr.resize(n); node *root = NULL; for(int j = 0; j < n; j++){ cin>>arr[j]; root = build(root, arr[j]); } if(arr[0] < 0 || !judgeBlackChild(root)|| !judgeBlackNum(root)) cout<<"No\n"; else cout<<"Yes\n"; } return 0; } |
参考
http://developer.51cto.com/art/201901/590926.htm