DFA最小化原理
所谓自动机的化简问题即是对任何一个确定有限自动机DFA M,构造另一个确定有限自动机DFA M’,有L(M)=L(M’),并且M’的状态个数不多于M的状态个数,而且可以肯定地说,能够找到一个状态个数为最小的M’。
下面首先来介绍一些相关的基本概念。
设Si是自动机M的一个状态,从Si出发能导出的所有符号串集合记为L(Si)。
设有两个状态Si和Sj,若有L(Si)=L(Sj),则称Si和Sj是等价状态。
上图所示的自动机中L(B)=L(C)={1},所有状态B和状态C是等价状态。
又例如终态导出的符号串集合中必然包含空串ε,而非终止状态导出的符号串集合中不可能包含空串ε,所以终态和非终止状态是不等价的。
对于等价的概念,我们还可以从另一个角度来给出定义。
给定一个DFA M,如果从某个状态P开始,以字符串w作为输入,DFA M将结束于终态,而从另一状态Q开始,以字符串w作为输入,DFA M将结束于非终止状态,则称字符串w把状态P和状态Q区分开来。
把不可区分开来的两个状态称为等价状态。
设Si是自动机M的一个状态,如果从开始状态不可能达到该状态Si,则称Si为无用状态。
设Si是自动机M的一个状态,如果对任何输入符号a都转到其本身,而不可能达到终止状态,则称Si为死状态。
化简DFA关键在于把它的状态集分成一些两两互不相交的子集,使得任何两个不相交的子集间的状态都是可区分的,而同一个子集中的任何两个状态都是等价的,这样可以以一个状态作为代表而删去其他等价的状态,然后将无关状态删去,也就获得了状态数最小的DFA。
下面具体介绍DFA的化简算法:
- 首先将DFA M的状态划分出终止状态集K1和非终止状态集K2。
K=K1∪K2
由上述定义知,K1和K2是不等价的。
- 对各状态集每次按下面的方法进一步划分,直到不再产生新的划分。
设第i次划分已将状态集划分为k组,即:
K=K1(i)∪K2(i)∪…∪Kk(i)
对于状态集Kj(i)(j=1,2,…,k)中的各个状态逐个检查,设有两个状态Kj’、 Kj’’∈Kj(i),且对于输入符号a,有:
F(Kj‘,a)=Km
F(Kj”,a)=Kn
如果Km和Kn属于同一个状态集合,则将Kj’和Kj’’放到同一集合中,否则将Kj’和Kj’’分为两个集合。
- 重复第(2)步,直到每一个集合不能再划分为止,此时每个状态集合中的状态均是等价的。
- 合并等价状态,即在等价状态集中取任意一个状态作为代表,删去其他一切等价状态。
- 若有无关状态,则将其删去。
根据以上方法就将确定有限自动机进行了简化,而且简化后的自动机是原自动机的状态最少的自动机。
Hopcroft算法原理
算法抽象:
- 1: Q/θ ← {F, Q − F}
- 2: while (∃U, V ∈ Q/θ, a ∈ Σ) s.t. Equation 1 holds do
- 3: Q/θ ← (Q/θ − {U}) ∪ {U ∩ δ^-1(V, a), U − U ∩ δ^-1(V, a)}
- 4: end while
算法细化:
- 1:W ← {F, Q − F} # 有些版本上只是 W ← {F }
- 2: P ← {F, Q − F}
- 3: while W is not empty do
- 4: select and remove S from W
- 5: for all a ∈ Σ do
- 6: la ← δ^-1(S, a)
- 7: for all R in P such that R ∩ la ≠ ∅ and R ∉ la do
- 8: partition R into R1 and R2: R1 ← R ∩ la and R2 ← R − R1
- 9: replace R in P with R1 and R2
- 10: if R ∈ W then
- 11: replace R in W with R1 and R2
- 12: else
- 13: if |R1| ≤ |R2| then
- 14: add R1 to W
- 15: else
- 16: add R2 to W
- 17: end if
- 18: end if
- 19: end for
- 20: end for
- 21: end while
流程图
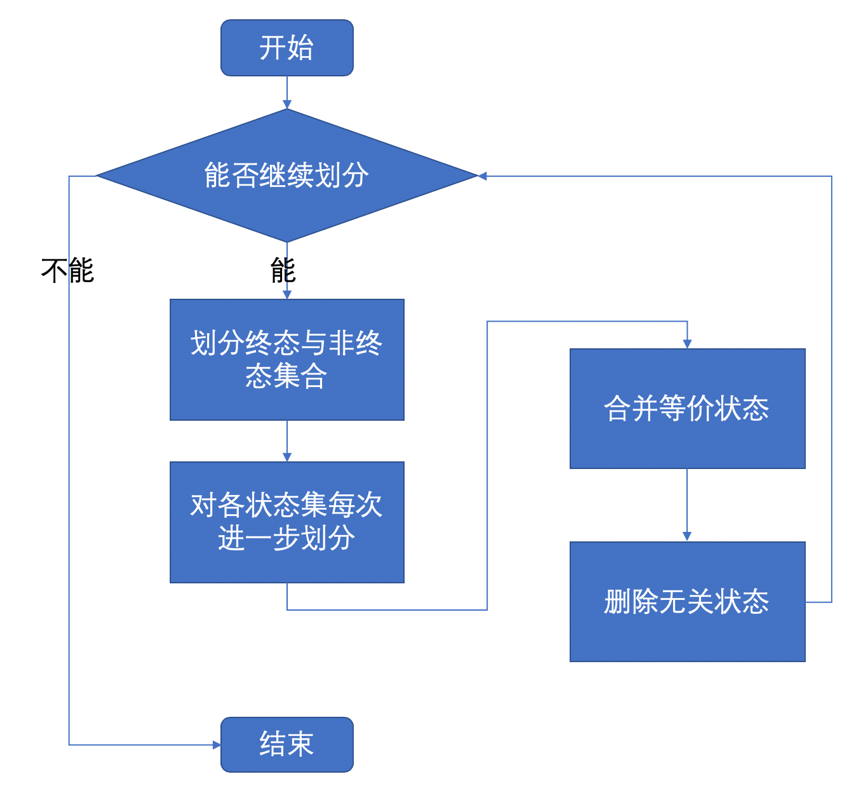
Python代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 |
from graphviz import Digraph import random from copy import deepcopy class Part: def __init__(self, src, edge, dst): self.src = src self.edge = edge self.dst = dst def move(DFA, src, edge): for i in range(len(DFA)): if DFA[i].src[0] == src and DFA[i].edge == edge: return DFA[i].dst[0] return '' def get_source_set(target_set, char, DFA): global allstatus allstatusSet = set(allstatus) source_set = set() for state in allstatusSet: try: if move(DFA, state, char) in target_set: source_set.update(state) except KeyError: pass return source_set def hopcroft_algorithm(DFA): global sigma global endSet global allstatus cins = set(sigma) termination_states = set(endSet) total_states = set(allstatus) not_termination_states = total_states - termination_states P = [termination_states, not_termination_states] W = [termination_states, not_termination_states] while W: A = random.choice(W) W.remove(A) for char in cins: X = get_source_set(A, char,DFA) P_temp = [] for Y in P: S = X & Y S1 = Y - X if len(S) and len(S1): P_temp.append(S) P_temp.append(S1) if Y in W: W.remove(Y) W.append(S) W.append(S1) else: if len(S) <= len(S1): W.append(S) else: W.append(S1) else: P_temp.append(Y) P = deepcopy(P_temp) return P def indexMinList(minList, a): for i in range(len(minList)): if a in minList[i]: return i return '' DFA = [] DFA2 = [] DFADic = {} sigma = ['a', 'b'] # dot = Digraph(comment='The Test Table') dot = Digraph("DFA") num = int(input('input:')) for i in range(num): x = input() y = input() z = input() temp = [] temp.append(x) temp.append(y) DFA2.append(temp) DFADic[tuple(temp)] = y temp = Part(x, y, z) DFA.append(temp) if i == 1: dot.node(name=x, color='blue') dot.edge(x, z, y) else: dot.node(name=x, color='black') dot.edge(x, z, y) for i in range(len(DFA)): print(DFA[i].src, DFA[i].edge, DFA[i].dst) endSet = [] endNum = int(input('input end num:')) for i in range(endNum): temp = input() endSet.append(temp) startSet = [] allSet = [] for i in range(len(DFA)): if DFA[i].src[0] not in endSet: startSet.append(DFA[i].src[0]) if DFA[i].dst[0] not in endSet: startSet.append(DFA[i].src[0]) allstatus = startSet allstatus.extend(endSet) dot.render('DFA.gv', view=True) minList = hopcroft_algorithm(DFA) minDFA = [] print(minList) for i in range(len(minList)): dstList = [0, 0] # 用来存储每种状态经过a和b变换后的结果 for j in range(len(minList[i])): listi = list(minList[i]) if dstList[0] == 0 and move(DFA, listi[j], sigma[0]) != '' and indexMinList(minList, move(DFA, listi[j], sigma[0])) != '': print(indexMinList(minList, move(DFA, listi[j], sigma[0]))) dstList[0] = min(minList[indexMinList(minList, move(DFA, listi[j], sigma[0]))]) # 使用Min函数的原因是为了重新给每种状态命名,选去每个状态中的最小的即可 if dstList[1] == 0 and move(DFA,listi[j], sigma[1]) != ''and indexMinList(minList, move(DFA, listi[j], sigma[1])) != '': dstList[1] = min(minList[indexMinList(minList, move(DFA, listi[j], sigma[1]))]) if dstList[0] != 0: temp = Part(min(minList[i]),'a',dstList[0]) minDFA.append(temp) if dstList[1] != 0: temp2 = Part(min(minList[i]), 'b', dstList[1]) minDFA.append(temp2) dot2 = Digraph('测试图片') for i in range(len(minDFA)): print(minDFA[i].src, minDFA[i].edge,minDFA[i].dst) if i == 1: dot2.node(name = minDFA[i].src, color='red') dot2.edge(minDFA[i].src, minDFA[i].dst, minDFA[i].edge) else: dot2.node(name=minDFA[i].src, color='black') dot2.edge(minDFA[i].src, minDFA[i].dst, minDFA[i].edge) dot2.render('minDFA.gv', view=True) |
测试
测试数据:
起始节点、边、终止节点的表示
共有14个边,7个节点
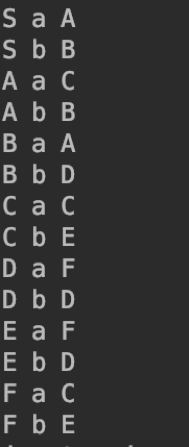
图形显示:
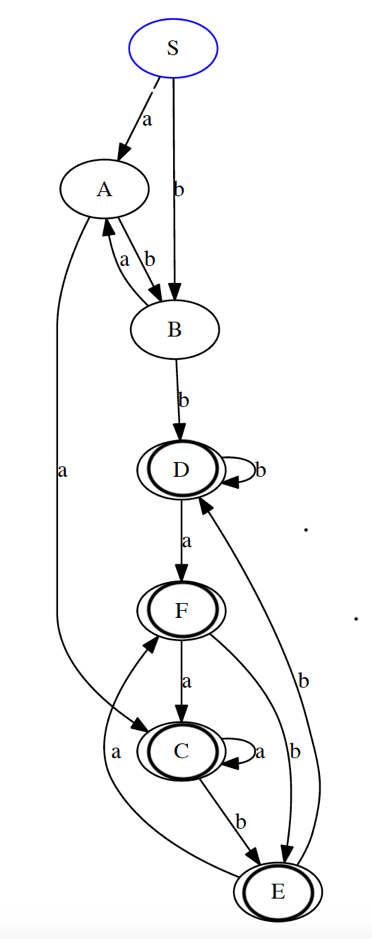
刚开始的子集为[{C,D,E,F},{S,A,B}]
实验结束后的结果:
![]()
最简化的DFA为:
C为终止节点,S为起始节点
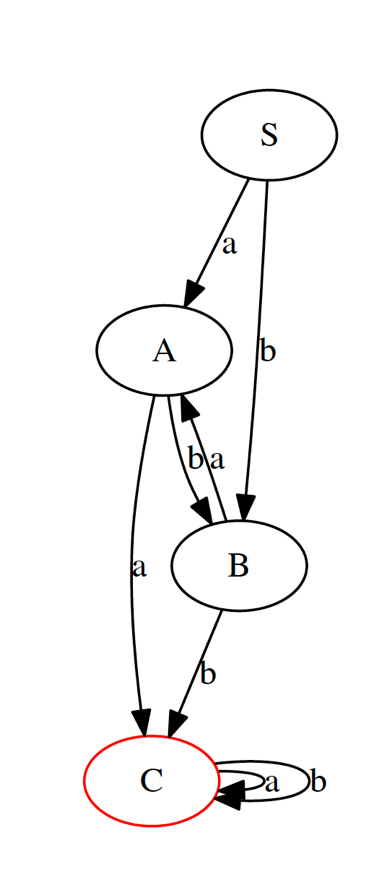
难点与解决的方法
- 在DFA最小化的过程中受限要去除无用状态,再使用子集分割算法处理。根据资料查找到一个快速的DFA最小化算法,叫做Hopcroft算法,通过该算法,能够处理不同大小字母表的DFA。
- 在进行子集分割算法后,要合并等价的节点并且重命名使用graphviz输出,在这一步,合并并重命名节点需要注意所有重复节点的入度和出度均要考虑,只有这样才能避免新的最小化的DFA的边不遗漏。





你好,你能解释一下程序的输入都是什么意思啊 我看了很久还是不明白。 主要是输入的end num 是什么呀?
我傻了, 知道了 但是出现了dot.render的错误。。。。
这个是画图,你可以把画图相关的去掉
您好,这个代码我发现好像只可以划分一次分组。
有的NFA划分一次就是最小DFA,有的NFA需要划分好几次才可以,代码里划分分组的函数(129行)没有循环判断。
例:
测试数据为:
0 a 1
0 b 2
1 a 3
1 b 0
2 a 5
2 b 2
3 a 3
3 b 6
4 a 1
4 b 2
5 b 6
6 a 5
endNum:6
分别为0 1 2 3 4 5
这个例子答案就是错误的。结果有6个状态,而正确的minDFA应该是三个状态。
不知道我说的对不对,您兴趣可以测试一下。
了解,第33行的函数应该没有问题,时间久远,如果您有新的想法欢迎指正。
请问X&Y和X-Y是什么意思啊?,为什么说我的S和S1没有定义呢?
我傻了,大家不要理我
牛!
想请教一下,dot.render()运行的时候总是报错:UnicodeDecodeError: ‘utf-8’ codec can’t decode byte 0xb2 in position 6: invalid start byte。修改了编码方式也不行。想请教一下您有没有遇到这个问题。
你把所有的汉字改成英文,注释也去掉
您好,修改过了,还是不行…