文章目录
一、引言
软件工程经济学中涉及软件项目与产品中的各项工程经济活动,如软件项目投资与筹资、招标与投标、项目可行性分析、项目任务分解、计划进度指定与团队组织建设、软件项目的成本、定价、效益以及经济、社会效果评价、风险分析、软件测试等工程经济参数间的关联分析与统计内容[1]。
而在任何软件的研发与管理都是在特定的时空范围内进行的,明确资金的时间价值的概念对软件项目以及企业的发展都具有重要意义。决策层若忽视了资金时间价值因素,就无法正确计算不同时期的软件项目收支,更无法正确评价投资活动的盈亏[2]。近年来,很多信息技术企业曾长期忽视资金时间价值理论的运用,资金使用效率低下,使得很多软件开发半途而废、舍本逐末,最终面临转型失败、决策失误的风险。比如,人人网、开心农场、锤子科技、中国移动飞信、中国雅虎等[3]。这些项目研发周期长,资金回收慢,投资效果差。因此,为了互联网企业更好地发展,需要把资金时间价值引入到软件研发中,在财务管理和生产经营活动等方面考虑这一因素,这是本文讨论的重点。
二、资金的时间价值理论概述
资金的时间价值:是指资金随着时间的推移而发生的增值,是资金周转使用后的增值额。它不仅受到通货膨胀补偿率的影响,而且还将受到投资利润率、风险补偿率的影响[4]。因此,不同时间点上的资金值不能直接相加,必须经过等值运算后才能相加,其中图1给出了一次收付型等值换算的终值公式图,P是现值,F是终值,利率为i,时间为n年。
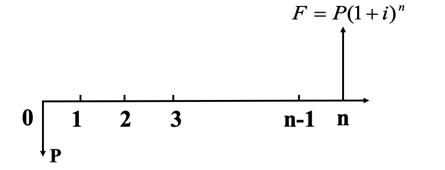 图1 一次收付型等值换算的终值公式图
图1 一次收付型等值换算的终值公式图
贴现:是指将发生在不同时点的现金金额全部换算成当前时刻t=0时的金额,这一换算过程称为“贴现”,将未来时点上的资金折现到现在时点上的资金之价值称为“现值”[5]。
折现率:是指将未来有限期预期收益折算成现值的比率。本金化率和资本化率或还原利率则通常是指将未来无限期预期收益折算成现值的比率。折现率不是利率,也不是贴现率,而是收益率。折现率的确定通常和当时的利率水平是有紧密联系的[5]。
现金流量:一定时期内(项目寿命期内)流入或流出项目系统的资金。其中,现金收入称为现金流入量(为正);现金支出称为现金流出量(为负),现金流入量与现金流出量之差称为净现金流量。为了准确地表达项目或投资方案的现金流量,应把投资项目或投资方案看做是一个独立的系统。其中定制型软件的现金流量图如图2所示。
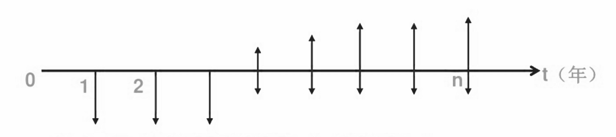
图2 定制型软件的现金流量图
三、资金的时间价值对风险软件项目的分析
成本效益分析的目的是从经济的角度评价开发一个软件项目是否可行。这一部分将根据大型的高风险软件项目的生命周期的进行基于资金的时间价值理论的成本效益分析。其中该项目的具体生命周期模型(螺旋模型)[6]如图2所示,在每个阶段开始时都需要进行风险分析,此种风险分析有多种方式,本文采用基于时间价值的分析。
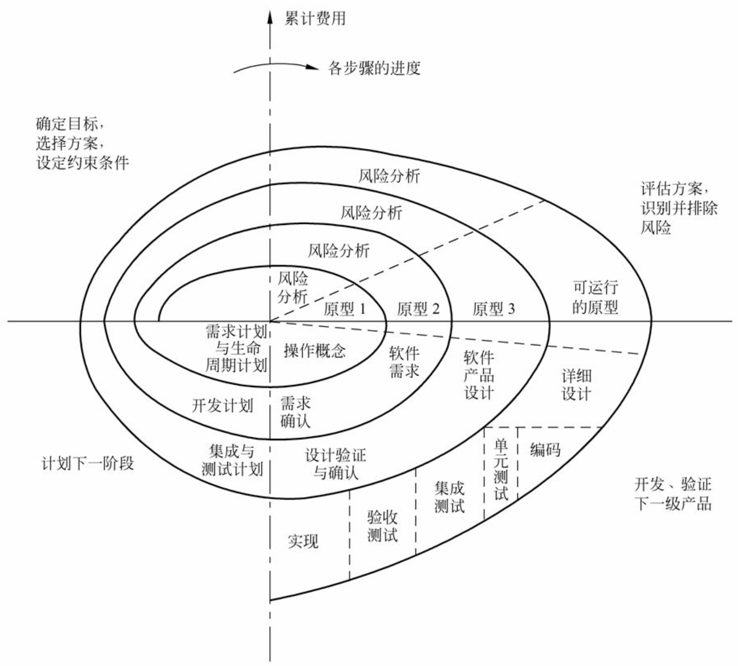
图3高风险软件项目的螺旋生命周期模型
3.1 成本效益分析的基本原理
成本效益分析是通过比较项目的全部成本和效益来评估项目价值的一种方法,成本—效益分析作为一种经济决策方法,将成本费用分析法运用于政府部门的计划决策之中,以寻求在投资决策上如何以最小的成本获得最大的收益。常用于评估需要量化社会效益的公共事业项目的价值。非公共行业的管理者也可采用这种方法对某一大型项目的无形收益(Soft benefits)进行分析。在该方法中,某一项目或决策的所有成本和收益都将被一一列出,并进行量化[1]。式(1)给出了度量指标。在此公式中,Bt指软件项目第t年的净收益,Ct指软件项目第t年的净支出,T指项目的寿命,i为平均贴现率,B指软件项目的总收益,C指软件项目的总支出,则用相对效果系数作为软件项目可行性的度量指标,当>1时,则可认为该大型软件项目是可以投资开发的。
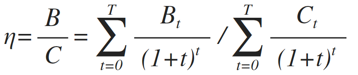
3.2 软件成本分析
按它们在项目生命周期中的出现阶段,首先对成本进行分类。主要可分为以下三类。
- (1)软件定义的成本:包括可行性分析、需求分析等。
- (2)软件开发的成本:包括开发软件的硬件支撑,参与开发项目的员工的工资和其他雇用成本及所有的相关成本。
- (3)运行与维护的成本:此部分成本占比最大,占软件研发[8]总成本的75%,甚至更多。
我们在成本效益分析时,我们需要将软件不同时期的软件成本转化为分析时(当前)的软件成本,如果往后投资每年的成本逐年递增时,需要用到等差流量的现值公式,下面的式子给出了计算方式。
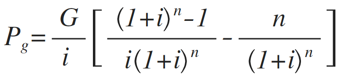
3.3 软件效益分析
软件效益项有多种类型,包含了直接经济效益和间接经济效益,其中直接经济效益包含以下几个方面:
- 产品成本降低
- 劳动生产率提高
- 流动资金周转加快
- 产品质量提高
- 库存周转加快
- 资源利用率提高
间接经济效益包括:
- 提高企业决策水平,提高员工的技能与素质
- 对用户服务水平的提高
- 文档的规范化与办公效率的提高
同样地,在分析软件效益时,也需要根据上述公式(2)进行计算。
3.4 基于净现值的分析
净现值法的基本思想是将软件项目寿命期内不同时期的投资(支出)和收益(收入)的现金流量根据资金的时间价值将其转换到参考点t=O(即贴现),并将这一系列贴现值累加起来,并定义其称为该项目现金流的净现值NPV[7]。若NPV大于零,说明从经济效益角度出发,项目可行;若NPV小于等于零,说明该软件项目从经济效益角度出发来看不可行,不值得投资。净现值NPV的计算公式如式(3)所示。其中CI为年收益,CO为年支出,ic为基准收益率。
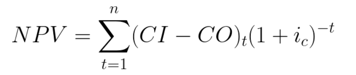
在一个大型的软件项目中,为了能够更好地反映项目的现金流量,我们需要对软件生命周期内的各种成本与收益进行细分,因此采用下面的公式(4)进行计算,具体的参数如表1所示。
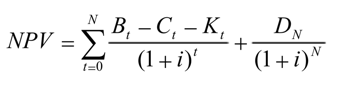
表1净现值NPV计算公式参数含义表
| 参数 | 含义 |
| NPV | 软件项目的净现值 |
| Bt | 软件项目在寿命期内t期的收益 |
| Ct | 软件项目在寿命期内t期的支出与成本 |
| Dt | 软件项目在寿命期内t期的残值 |
| Kt | 软件项目在寿命期内t期的投资额 |
| N | 软件项目使用年限 |
| i | 基准体现率 |
举例来说,某一具体软件的现金流量图如图4所示,可以看到前几年投资均为100万元,到了第四年时有了收益,往后5年的收益将持续增加。则其项目现金流量表如表2所示。
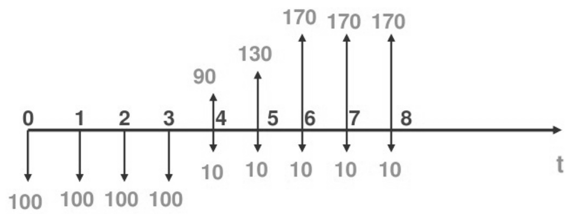
图4某一具体软件的现金流量图
表2 某一项目的现金流量表
| t | Kt | Bt | Ct |
| 0
1 2 3 |
100
100 100 100 |
\
\ \ \ |
\
\ \ \ |
| 4
5 6 7 8 |
\
\ \ \ \ |
90
130 170 170 170 |
10
10 10 10 10 |
根据式(3)和表2计算可知,NPV大于零,因此说明从经济效益角度出发,该软件项目可行。
当有两个软件项目可供实施时,项目A的所有投资(支出)的贴现值为400万,NPV为7O万,项目B的所有投资的贴现值为90万,NPV为3O万,如果两个软件项目的生命周期相同,那么,哪一个更值得投资呢?这就需要净现值率 NPVR的概念来计算,计算公式如式(5)所示,单位投资额的净现值越大,表示单位投资回报率越大。
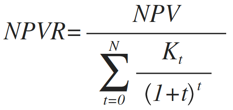
表3 项目A与项目B的NPVR比较
| NPVR | |
| 项目A | 70/400*100%=17.5% |
| 项目B | 30/90*100%=33.3% |
通过表3的结果可以看出,项目B的NPVR较高,因此该项目的投资回报率较大,经济上讲比A更优。
在经过了成本、效益与净现值的分析后,我们需要根据这些数据来具体绝对软件项目的总体开发方案。当然也不能简单地进行分析,还得从多个角度进行比较,确保软件项目不会使企业亏损。3.5介绍了更多的方法。
3.5 其他方法
在大型软件项目经济效益分析的方法中,还包括内部收益率法与投资回收期法。
内部收益率法是一种通过求解使工程项目方案达到收支平衡时的对应临界贴现率it,并将it与基准贴现率或最低期望盈利率(由投资者确定)it相比较来决定工程项目是否值得投资的一种评价方法。
所谓工程项目的投资回收期是指将该工程项目的投资以净收益的形式全部收回的时间。它反映了能将项目投资得到补偿(回报)的速度(单位为年)。投资回收期法是通过给定工程项目的投资回收期的求解,并将其与行业基准投资回收期作比较来判决该投资项目的可行性的一种评价方法。常用的有静态投资回收期法和动态投资回收期法。
以上两种方法具体的操作措施可以参考论文[1],在此便不再赘述。
四、结语
在一个大型高风险的软件项目中,不能简单地在一个时间状态下静态分析。正确的做法应该是在软件生命周期的每一个阶段都应该做好基于资金时间价值的风险与成本效益分析,如果某一个经济指标有变动,需要提前做好准备,一旦分析发现该软件项目不可行,应该立即停止软件项目的开发,以免企业遭受更大的损失。
参考文献
- [1] 岳清. 软件工程经济学中软件项目经济效益分析方法的探讨[J]. 大众科技, 2012, 14(4):250-252.
- [2] 李双全. 浅谈软件项目管理中的成本效益分析和收益管理[J]. 科技资讯, 2012(9):175-175.
- [3] 互联网公司失败案例大盘点[DB/0L]https://www.yelunet.com/chuangye/2018-01-22/799.html,2018
- [4] 曹艳华. 资金时间价值理论及其在现代企业中的应用[J]. 黑龙江科技信息, 2007(12):112-112.
- [5] 卢晓勇, 陈木生. 软件工程经济学中软件成本估算方法探讨[J]. 中国教育信息化, 2006(23):68-70.
- [6] Iivari J. A hierarchical spiral model for the software process[J]. Acm Sigsoft Software Engineering Notes, 1987, 12(1):35-37.
- [7] 李心愉. 净现值法和内部收益率法的比较法分析[J]. 数量经济技术经济研究, 1998(12):32-34.
- [8] Boehm B W. Software Engineering[J]. IEEE Transactions on Computers, 2006, C-25(12):1226-1241.