作为一个编程菜鸡,先刷刷前几题,八道题目争取6题有思路,5题能写出来,3题能AC(大佬勿嘲笑)。由于部分题目已经关闭,无法看到是否AC(以下代码可能无法通过全部测试用例),如有错误,请指出,O(∩_∩)O谢谢。
地址:
http://bailian.openjudge.cn/xly2018/
A:计算两个日期之间的天数
全局题号7595 提交次数663 尝试人数225 通过人数211
- 总时间限制:
- 1000ms
- 内存限制:
- 65536kB
- 描述
- 给定两个日期,计算相差的天数。比如2010-1-1和2010-1-3相差2天。
- 输入
- 共两行:
第一行包含三个整数startYear,startMonth,startDay,分别是起始年、月、日。
第二行包含三个整数endYear,endMonth,endDay,分别是结束年、月、日。
相邻两个整数之间用单个空格隔开。年份范围在1~3000。保证日期正确且结束日期不早于起始日期。 - 输出
- 输出一个整数,即是两个日期相差的天数。
- 样例输入
-
122008 1 12009 1 1
- 样例输出
-
1366
- 提示
- 闰年被定义为能被4整除的年份,但是能被100整除而不能被400整除的年是例外,它们不是闰年。闰年的2月份有29天。
C++实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
#include<cstdio> /* 第一行包含三个整数startYear,startMonth,startDay,分别是起始年、月、日。 第二行包含三个整数endYear,endMonth,endDay,分别是结束年、月、日。 */ int leappp(int n){ if((n % 4 == 0 && n % 100 != 0) || n % 400 == 0)return 1; return 0; } int month[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; int main(){ int startYear, startMonth, startDay; int endYear, endMonth, endDay; int res = 0; scanf("%d%d%d", &startYear, &startMonth, &startDay); scanf("%d%d%d", &endYear, &endMonth, &endDay); if(startYear == endYear){ if(startMonth == endMonth){ printf("%d\n", endDay - startDay); return 0; }else{ for(int i = startMonth; i < endMonth; i++){ if(i == 2)res += leappp(startYear); res += month[i - 1]; } res = res - startDay + endDay; printf("%d\n", res); } }else{ for(int i = startYear; i < endYear; i++){ res += 365 + leappp(i); } int prestart = 0; for(int i = 1; i < startMonth; i++){ if(i == 2)prestart += leappp(startYear); prestart += month[i]; } prestart += startDay; res -= prestart; for(int i = 1; i < endMonth; i++){ if(i == 2)res += leappp(endYear); res += month[i]; } res += endDay; printf("%d\n", res); } return 0; } |
-
B:回文子串
全局题号17415 提交次数450 尝试人数215 通过人数199
- 动态规划
- 总时间限制:
- 1000ms
- 内存限制:
- 65536kB
- 描述
- 给定一个字符串,寻找并输出字符串中最长回文子串。回文串即从左到右和从右到左读都一样的字符串。
如果字符串中包含多个回文子串,则返回第一个。 - 输入
- 第一行是整数n,字符串的个数(n < 20)
- 输出
- 接下来n行,每行一个字符串
字符串的长度不超过100 - 样例输入
-
12343abbabadecscdedcd
- 样例输出
-
123ababcdedc
C++实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#include<iostream> #include<vector> using namespace std; string work(string str){ if(str.size() < 2)return str; bool dp[101][101]; int start = 0, len = 1; for(int i = 0; i < str.size(); i++){ dp[i][i] = true; if(i < str.size() - 1 && str[i] == str[i + 1])dp[i][i + 1] = dp[i + 1][i] = true; for(int j = i - 1; j >= 0; j--){ if(str[i] == str[j]){ dp[i][j] = dp[i - 1][j + 1]; if(dp[i][j] && i - j + 1 > len){ start = j; len = i - j + 1; } } } } return str.substr(start, len); } int main(){ int T; string str; cin>>T; while(T--){ cin>>str; cout<<work(str)<<endl; } return 0; } |
C:The Die Is Cast
全局题号483 提交次数293 尝试人数77 通过人数39
DFS回溯
- 总时间限制:
- 1000ms
- 内存限制:
- 65536kB
- 描述
- InterGames is a high-tech startup company that specializes in developing technology that allows users to play games over the Internet. A market analysis has alerted them to the fact that games of chance are pretty popular among their potential customers. Be it Monopoly, ludo or backgammon, most of these games involve throwing dice at some stage of the game.
Of course, it would be unreasonable if players were allowed to throw their dice and then enter the result into the computer, since cheating would be way to easy. So, instead, InterGames has decided to supply their users with a camera that takes a picture of the thrown dice, analyzes the picture and then transmits the outcome of the throw automatically.For this they desperately need a program that, given an image containing several dice, determines the numbers of dots on the dice.We make the following assumptions about the input images. The images contain only three different pixel values: for the background, the dice and the dots on the dice. We consider two pixels connected if they share an edge - meeting at a corner is not enough. In the figure, pixels A and B are connected, but B and C are not.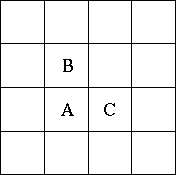
A set S of pixels is connected if for every pair (a,b) of pixels in S, there is a sequence a1, a2, ..., ak in S such that a = a1 and b = ak , and ai and ai+1 are connected for 1 <= i < k.We consider all maximally connected sets consisting solely of non-background pixels to be dice. `Maximally connected' means that you cannot add any other non-background pixels to the set without making it dis-connected. Likewise we consider every maximal connected set of dot pixels to form a dot.
- 输入
- The input consists of pictures of several dice throws. Each picture description starts with a line containing two numbers w and h, the width and height of the picture, respectively. These values satisfy 5 <= w, h <= 50.
The following h lines contain w characters each. The characters can be: "." for a background pixel, "*" for a pixel of a die, and "X" for a pixel of a die's dot.
Dice may have different sizes and not be entirely square due to optical distortion. The picture will contain at least one die, and the numbers of dots per die is between 1 and 6, inclusive.
The input is terminated by a picture starting with w = h = 0, which should not be processed.
- 输出
- For each throw of dice, first output its number. Then output the number of dots on the dice in the picture, sorted in increasing order.
Print a blank line after each test case.
- 样例输入
-
123456789101112131415161730 15...........................................................................*.................*****......****...............*X***.....**X***..............*****....***X**...............***X*.....****................*****.......*....................................................***........******............**X****.....*X**X*...........*******......******..........****X**.......*X**X*.............***........******...................................0 0
- 样例输出
-
12Throw 11 2 2 4
C++实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
#include<iostream> #include<cstdio> #include<vector> #include<algorithm> using namespace std; int sum; int m, n; char v[55][55]; int go[][2] = {0, 1, 0, -1, 1, 0, -1, 0}; void DFSX(int x, int y){ //目的是将相邻的X换成* v[x][y] = '*'; for(int i = 0; i < 4; i++){ int nx = x + go[i][0]; int ny = y + go[i][1]; if(nx < 0 || nx > m - 1 || ny < 0 || ny > n - 1)continue; if(v[nx][ny] == 'X')DFSX(nx, ny); } } void DFSstar(int x, int y){ v[x][y] = '.'; for(int i = 0; i < 4; i++){ int nx = x + go[i][0]; int ny = y + go[i][1]; if(nx < 0 || nx > m - 1 || ny < 0 || ny > n - 1)continue; if(v[nx][ny] == 'X'){ DFSX(nx, ny); sum++; //相邻的X换成*号后就只有1个了 } if(v[nx][ny] == '*')DFSstar(nx, ny); //如果是*就继续搜索,直到将所有点都搜完 } } int main(){ int t = 1; while(cin>>n>>m){ if(m == 0 || n == 0)break; vector<int> ans; for(int i = 0; i < m; i++){ scanf("%s", v[i]); } for(int i = 0; i < m; i++){ for(int j = 0; j < n; j++){ if(v[i][j] == '*'){ sum = 0; DFSstar(i, j); ans.push_back(sum); } } } sort(ans.begin(), ans.end()); cout<<"Throw "<<t<<endl; t++; for(int i = 0; i < ans.size(); i++){ printf("%d%s", ans[i], i == ans.size() - 1 ? "\n\n" : " "); } } return 0; } |
D:Euro Efficiency
动态规划
全局题号254 提交次数90 尝试人数35 通过人数17
- 总时间限制:
- 1000ms
- 内存限制:
- 65536kB
- 描述
- On January 1st 2002, The Netherlands, and several other European countries abandoned their national currency in favour of the Euro. This changed the ease of paying, and not just internationally.
A student buying a 68 guilder book before January 1st could pay for the book with one 50 guilder banknote and two 10 guilder banknotes, receiving two guilders in change. In short:50+10+10-1-1=68. Other ways of paying were: 50+25-5-1-1, or 100-25-5-1-1.Either way, there are always 5 units (banknotes or coins) involved in the payment process, and it
could not be done with less than 5 units.
Buying a 68 Euro book is easier these days: 50+20-2 = 68, so only 3 units are involved.This is no coincidence; in many other cases paying with euros is more efficient than paying with guilders. On average the Euro is more efficient. This has nothing to do, of course, with the value of the Euro, but with the units chosen. The units for guilders used to be: 1, 2.5, 5, 10, 25, 50,whereas the units for the Euro are: 1, 2, 5, 10, 20, 50.
For this problem we restrict ourselves to amounts up to 100 cents. The Euro has coins with values 1, 2, 5, 10, 20, 50 eurocents. In paying an arbitrary amount in the range [1, 100] eurocents, on average 2.96 coins are involved, either as payment or as change. The Euro series is not optimal in this sense. With coins 1, 24, 34, 39, 46, 50 an amount of 68 cents can be paid using two coins.The average number of coins involved in paying an amount in the range [1, 100] is 2.52.
Calculations with the latter series are more complex, however. That is, mental calculations.These calculations could easily be programmed in any mobile phone, which nearly everybody carries around nowadays. Preparing for the future, a committee of the European Central Bank is studying the efficiency of series of coins, to find the most efficient series for amounts up to 100 eurocents. They need your help.
Write a program that, given a series of coins, calculates the average and maximum number of coins needed to pay any amount up to and including 100 cents. You may assume that both parties involved have sufficient numbers of any coin at their disposal. - 输入
- The first line of the input contains the number of test cases. Each test case is described by 6 different positive integers on a single line: the values of the coins, in ascending order. The first number is always 1. The last number is less than 100.
- 输出
- For each test case the output is a single line containing first the average and then the maximum number of coins involved in paying an amount in the range [1, 100]. These values are separated by a space. As in the example, the average should always contain two digits behind the decimal point. The maximum is always an integer.
- 样例输入
-
123431 2 5 10 20 501 24 34 39 46 501 2 3 7 19 72
- 样例输出
-
1232.96 52.52 32.80 4
C++实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#include<iostream> #include<vector> #include<algorithm> using namespace std; vector<int> coins(6); int min(int a, int b){ return a < b ? a : b; } int main(){ int t; cin>>t; while(t--){ int dp[101], max_ = 0; double ave = 0; for(int i = 0; i < 6; i++){ cin>>coins[i]; } for(int i = 1; i <= 100; i++) dp[i] = 999; for(int i = 0; i < 6; i++){ for(int j = coins[i]; j <= 100; j++){ dp[j] = min(dp[j], dp[j - coins[i]]+1); } } for(int i = 0; i < 6; i++){ for(int j = 100 - coins[i]; j >= 1; j--){ dp[j] = min(dp[j], dp[j + coins[i]]+1); } } for(int i = 1; i <= 100; i++){ ave += dp[i]; max_ = max_ > dp[i] ? max_ : dp[i]; } printf("%.2f %d\n", ave/100, max_); } return 0; } |



Euro Efficiency中动态规划的二重循环次数不够,无法仿真高面值货币的情况,建议j的范围到2000