设文法G[S]=(VN,VT,P,S),则首字符集为:
FIRST(α)={a | αaβ,a∈VT,α,β∈V *}。
若αε,ε∈FIRST(α)。
由定义可以看出,FIRST(α)是指符号串α能够推导出的所有符号串中处于串首的终结符号组成的集合。所以FIRST集也称为首符号集。
设α=x1x2…xn,FIRST(α)可按下列方法求得:
令FIRST(α)=Φ,i=1;
- 若xi∈VT,则xi∈FIRST(α);
- 若xi∈VN;
① 若εFIRST(xi),则FIRST(xi)∈FIRST(α);
② 若ε∈FIRST(xi),则FIRST(xi)-{ε}∈FIRST(α);
- i=i+1,重复(1)、(2),直到xi∈VT,(i=2,3,…,n)或xi∈VN且若εFIRST(xi)或i>n为止。
当一个文法中存在ε产生式时,例如,存在A→ε,只有知道哪些符号可以合法地出现在非终结符A之后,才能知道是否选择A→ε产生式。这些合法地出现在非终结符A之后的符号组成的集合被称为FOLLOW集合。下面我们给出文法的FOLLOW集的定义。
设文法G[S]=(VN,VT,P,S),则
FOLLOW(A)={a | S… Aa …,a∈VT}。
若S…A,#∈FOLLOW(A)。
由定义可以看出,FOLLOW(A)是指在文法G[S]的所有句型中,紧跟在非终结符A后的终结符号的集合。
FOLLOW集可按下列方法求得:
- 对于文法G[S]的开始符号S,有#∈FOLLOW(S);
- 若文法G[S]中有形如B→xAy的规则,其中x,y∈V *,则FIRST(y)-{ε}∈FOLLOW(A);
- 若文法G[S]中有形如B→xA的规则,或形如B→xAy的规则且ε∈FIRST(y),其中x,y∈V *,则FOLLOW(B)∈FOLLOW(A);
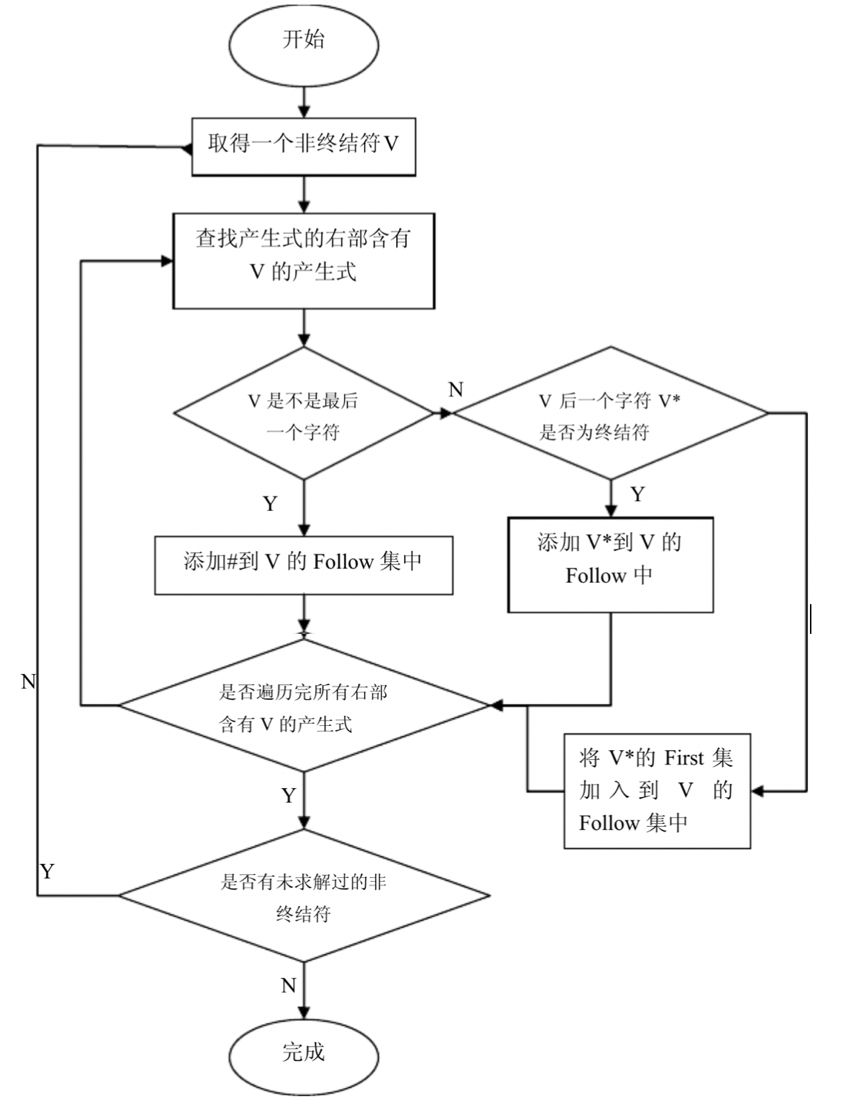
求First集合的流程图:

求follow集合的流程图:
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 |
#include<iostream> #include<string> #include<algorithm> #include<stdio.h> using namespace std; #define MAX 50 int NONE[MAX] = { 0 }; string strings; //产生式 string Vn; //非终结符 string Vt; //终结符 string first[MAX]; //存放每个终结符的first集 string First[MAX]; //存放每个非终结符的first集 string Follow[MAX]; //存放每个非终结符的follow集 int N; //产生式个数 struct STR { string left; string right; }; void rec(STR *p) //识别Vn和Vt { int i, j; for (i = 0;i < N;i++) //第i个产生式 { for (j = 0;j < (int)p[i].left.length();j++)//左侧 { if ((p[i].left[j] >= 'A'&&p[i].left[j] <= 'Z')) //左侧第j个字母是大写 { if (Vn.find(p[i].left[j])>100) //Vn里没找到返回很大的值 Vn += p[i].left[j]; } else { if (Vt.find(p[i].left[j])>100) //小写字母放Vt Vt += p[i].left[j]; } } for (j = 0;j < (int)p[i].right.length();j++)//右侧 { if (!(p[i].right[j] >= 'A'&&p[i].right[j] <= 'Z')) { if (Vt.find(p[i].right[j])>100) Vt += p[i].right[j]; } else { if (Vn.find(p[i].right[j]) > 100) Vn += p[i].right[j]; } } } } void getlr(STR *p, int i) //将产生式的左右部分别放入left,right { int j; for (j = 0;j<strings.length();j++) { if (strings[j] == '-'&&strings[j + 1] == '>') { p[i].left = strings.substr(0, j); p[i].right = strings.substr(j + 2, strings.length() - j); } } } string Letter_First(STR *p, char ch) { int t; if (!(Vt.find(ch)>100)) //在Vt里,first就是自身 { first[Vt.find(ch)] = ch; return first[Vt.find(ch) - 1]; } if (!(Vn.find(ch) > 100)) //在Vn中的第i个 { for (int i = 0;i < N;i++) //第i个产生式 { if (p[i].left[0] == ch) //左侧字符是ch { if (!(Vt.find(p[i].right[0])>100)) { if (First[Vn.find(ch)].find(p[i].right[0]) > 100) //右侧第一个字符是Vt,加入Vni的first集合中 { First[Vn.find(ch)] += p[i].right[0]; } } if (p[i].right[0] == '#') { if (First[Vn.find(ch)].find('#') > 100) //右侧第一个字符是空,加入Vni的first集合中 { First[Vn.find(ch)] += '#'; } } if (!(Vn.find(p[i].right[0]) > 100)) //右侧第一个字母是Vn { if (p[i].right.length() == 1) //只有一个字母 { string ff; ff = Letter_First(p, p[i].right[0]); //把右侧字母的first集合加入到左侧字母中 for (int k = 0;k < ff.length();k++) { if (First[Vn.find(ch)].find(ff[k])>100) { First[Vn.find(ch)] += ff[k]; } } } else //多个字母都是Vn { for (int j = 0;j < p[i].right.length();j++) { string TT; TT = Letter_First(p, p[i].right[j]); if (!(TT.find('#')>100) && (j + 1) < p[i].right.length()) //右侧非末位字母的first集里有空 { for (int t = 0;t < TT.length();t++) { if (TT[t] != '#'&&First[Vn.find(ch)].find(TT[t])>100) //右侧字母的无空first集加入到Vni的first集 First[Vn.find(ch)] += TT[t]; } //cout << p[i].right[j]<<"already "; } else //集合里无空或有空但是最后一个,直接加入 { for (t = 0;t < TT.length();t++) { if (First[Vn.find(ch)].find(TT[t])>100) First[Vn.find(ch)] += TT[t]; } break; } } } } } } return First[Vn.find(ch)]; } } string Letter_Follow(STR *p, char ch) { int t, k; NONE[Vn.find(ch)]++; //扫过1遍 if (NONE[Vn.find(ch)] == 2) { NONE[Vn.find(ch)] = 0; return Follow[Vn.find(ch)]; //第二次扫到,直接返回 } for (int i = 0;i < N;i++) { for (int j = 0;j < p[i].right.length();j++) { if (p[i].right[j] == ch) //右侧扫描到A { if (j + 1 == p[i].right.length()) //A是末尾 S->aA { string gg; gg = Letter_Follow(p, p[i].left[0]); // NONE[Vn.find(p[i].left[0])] = 0; //NONE[S]=0 A->aA NONE[A]置0重扫 for (int k = 0;k < gg.length();k++) { if (Follow[Vn.find(ch)].find(gg[k])>100) //S的follow加入到A中 { Follow[Vn.find(ch)] += gg[k]; } } } else //A不是末尾 S->AB { string FF; for (int m = j + 1;m < p[i].right.length();m++) { string TT; TT = Letter_First(p, p[i].right[m]); if (!(TT.find('#') > 100) && (m + 1) < p[i].right.length()) //A后面的Vn的first集有空且不是最后一个 { for (t = 0;t < TT.length();t++) { if (FF.find(TT[t])>100 && TT[t] != '#') //去掉空加入 FF += TT[t]; } } else { //first集没有空或者最后一个有空 for (t = 0;t < TT.length();t++) { if (FF.find(TT[t])>100) FF += TT[t]; } break; //没空的直接break } } if (FF.find('#') > 100) { for (k = 0;k < FF.length();k++) { if (Follow[Vn.find(ch)].find(FF[k])>100) Follow[Vn.find(ch)] += FF[k]; } } else { for (k = 0;k < FF.length();k++) { if ((Follow[Vn.find(ch)].find(FF[k])>100) && FF[k] != '#') { Follow[Vn.find(ch)] += FF[k]; } } string dd; dd = Letter_Follow(p, p[i].left[0]); //最后一个有空 S的follow加入A的follow //NONE[Vn.find(p[i].left[0])] = 0; for (k = 0;k < dd.length();k++) { if (Follow[Vn.find(ch)].find(dd[k])>100) { Follow[Vn.find(ch)] += dd[k]; } } } } } } } return Follow[Vn.find(ch)]; } int main() { int i, j, k; cout << "请输入产生式总数:"; cin >> N; cout << "\n请输入各产生式(#代表空):" << endl; STR *p = new STR[MAX]; for (i = 0;i < N;i++) { cin >> strings; getlr(p, i); } rec(p); cout << endl; cout << "\n=========================================" << endl; cout << "非终结符" << "\t" << "FIRST" << "\t\t" << "FOLLOW" << endl; for (i = 0;i < Vn.length();i++) { cout << " " << Vn[i] << "\t\t{"; string pp; pp = Letter_First(p, Vn[i]); for (j = 0;j + 1 < pp.length();j++) { cout << pp[j] << ","; } cout << pp[pp.length() - 1] << "} "; Follow[0] += '$'; //开始符加入$ cout << " {"; string ppp; ppp = Letter_Follow(p, Vn[i]); for (k = 0;k + 1 < ppp.length();k++) { cout << ppp[k] << ","; } cout << ppp[ppp.length() - 1] << "}" << endl; } cout << "\n=========================================" << endl; return 0; } |
实验
测试数据:
- S->AB
- S->bC
- A->~
- A->b
- B->~
- B->aD
- C->AD
- C->b
- D->aS
- D->c
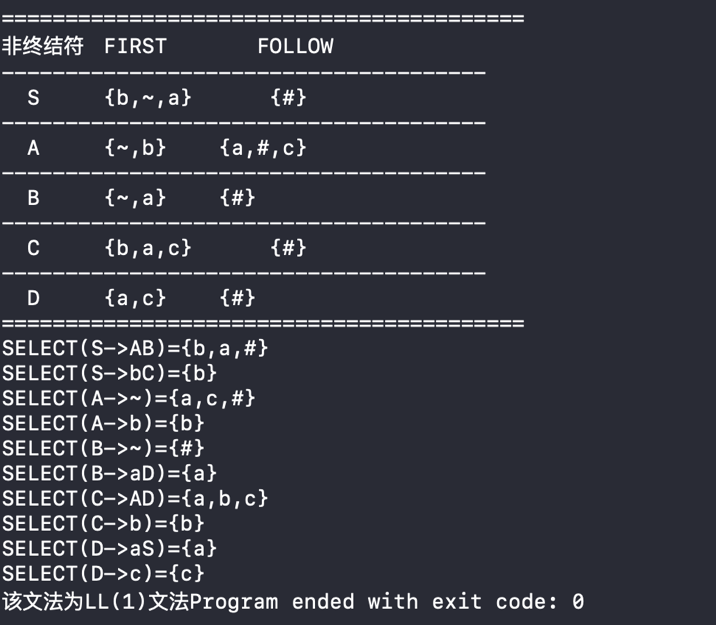
结果:
问题和难点
- 本次实验使用需要计算非终结符的first和follow集合,在求解过程中,如果遇到类似FOLLOW(A)=FOLLOW(B)的情况,此时,B的FOLLOW集合还未求解,因此需要使用递归调用solveFollow的函数。
- 由于本次是上下文无关的文法,不是正规文法求解集合,因此需要要注意文法产生式右部长度大于等于3的情况,这种情况可以在求解程序中一个一个分析产生式的右部。这样才能保证不遗漏。


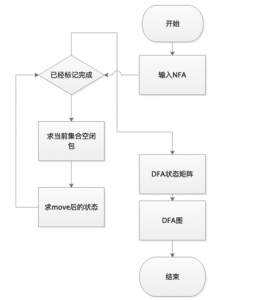
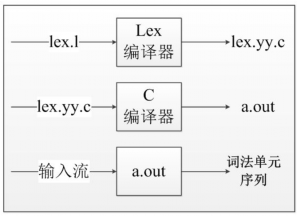

思路非常好。借助了博主的算法,成功实现了自己的语法分析器
棒棒棒!!!!