基于进化计算的NP难题求解的研究综述

摘要

进化算法作为一种随机优化算法在复杂函数优化、组合优化与路径规划等领域具有广泛的应用。本文从进化算法的发展现状、缺陷与改进等方面进行了细致的分析调研。具体介绍了NP问题的定义与研究成果，并研究与讨论了基于传统经典与最新前沿的进化算法解决带约束组合优化的NP难题的方法策略。在标准数据集上的实验结果表明，进化算法在求解NP问题具有一定的实用性与延展性。

关键词：进化计算；NP难问题；遗传算法；群智能；多目标优化

A Review of NP Problem Solving Based on Evolutionary Computation

Abstract: As a stochastic optimization algorithm, evolutionary algorithm is widely used in the fields of complex function optimization, combinatorial optimization and path planning. This paper makes a detailed analysis and investigation on the development status, defects and improvement of evolutionary algorithms. The definition and research results of NP problem are introduced in detail while the methods and strategies of solving constrained NP problem based on classical and latest evolutionary algorithms are studied and discussed in combinatorial optimization. Experimental results on the standard data set show that the evolutionary algorithm is practical and extensible in solving NP hard problems.

Key Words: evolutionary computing; NP problem; genetic algorithm; swarm intelligence; multi-objective optimization

一、演化计算

1.1 进化计算的历史及现状

20世界50年代，当电脑性能还远远落后时，达尔文的进化论就被应用于自动问题的解决^[1]。在美国，Fogel提出了进化编程的思想 ^[2]，也就是后来所谓的遗传算法（GA）。GA算法是受生物进化过程中“优胜劣汰”的自然选择机制和遗传信息的传递规律的影响，通过程序迭代模拟这一过程，把要解决的问题看作环境，在一些可能的解组成的种群中，通过自然演化寻求最优解^[3]，这些理论大约独自发展了15年。

在80年代之前，并没有引起人们太大的关注，因为它本身还不够成熟，而且受到了当时计算机容量小、运算速度慢的限制，并没有发展出实际的应用成果。

到了20世纪90年代初，遗传编程（GP）^[4]也被提出，于是以遗传算法、遗传编程、进化策略与进化规划为代表的进化计算作为一个学科开始正式出现，融合出了新的进化算法，促进了机器学习领域的巨大发展。与此同时，在基于达尔文进化论的思想上，变体的进化算法要层出不穷、方兴未艾，如粒子群算法（PSO）^[5]、蚁群算法（ACO）^[6]、人工蜂群算法（ABC）^[7]等，这些算法都是基于群智能的随机优化算法，在很多领域都广泛的应用。

1.2 传统的进化计算分类

传统的进化计算有四种类别，他们分别是遗传算法、遗传编程、进化策略与进化规划^[1]。在这一部分，我们将着重讨论遗传算法。

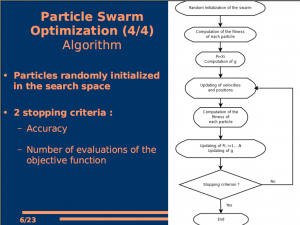
遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码(一般来说包含实数编码与二进制编码)的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现是某种基因组合，它决定了个体的形状的外部表现。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代进化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。单目标领域有经典的GA算法，多目标领域有基于快速非支配排序与拥挤距离选择的NSGA2算法^[8]。 算法1给出了基本遗传算法的伪码。

进化策略与进化编程作为一种求解参数优化问题的方法，模仿生物进化原理，假设不论基因发生何种变化，产生的结果（性状）总遵循零均值、某一方差的高斯分布。

遗传规划的实是用广义的层次化计算机程序描述问题比较适合求解一类由于各种不确定性因素导致的复杂非线性问题。

1.3 基于群智能的算法（以PSO为代表）

由于进化计算具有策略的灵活性和对问题的适应性，科学和工程领域经常用来解决优化问题，相对于经典优化算法，进化计算通常有很大的优势。

其中，基于群智能的PSO算法是由Kennedy和Eberhart提出的，这是一种随机优化算法^[5]。在粒子群算法中，每个粒子有位置向量和速度向量，位置向量代表着一个候选解，速度向量代表该粒子下一代需要移动的速度与方向。每个向量都是有n个实数值组成，n是当前问题的维度。每个粒子通过适应度函数值来估计其优劣程度，每个粒子搜索到的最优解称为pbest（局部最优解），整个粒子群所有代中搜索的最优解称为gbest（全局最优解）

粒子的位置和速度通过以下公式（1）和（2）进行更新：

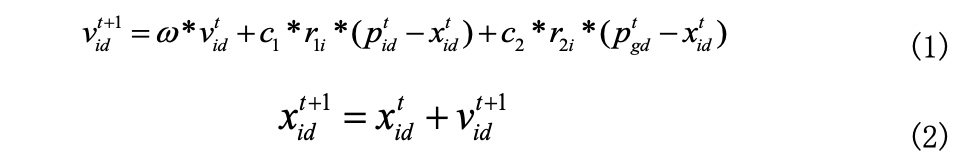
其中和是第i个粒子第d个维度在时间t的值，和是在[0,1]之间的加速常数。粒子群算法具有速度快，效率高，适合实数值优化等特点，但是在处理高维数据，尤其是多峰问题时容易陷入局部最优。针对此种情况，有大量的研究与工作来处理这种问题^[10,11,12]。

粒子群算法的伪码如算法2所示。

1.4 进化算法的局限性与改进

在当今大数据时代，数据的规模大且维度高。在大规模高维优化问题中，普通的进化算法很容易陷入局部最优，例如高维旅行商问题，当城市的维度大于100时，优化是非常困难的；在特征选择问题中，当特征的维度达到10000维以上时，由于特征的冗余与不相关性，不但容易陷入局部最优，而且计算时间消耗难以想象，想要优化基本不可能。

因此对于大规模数据因此对于进化算法来说需要依赖有效地全局搜索技术与问题求解的分治代理技术^[18]。

对于陷入局部最优的问题，科研工作者提出了很多的方法，例如由Storn等人在1995提出的差分进化算法^[19]（Differential Evolution），和其它进化算法一样，DE是一种模拟生物进化的随机模型，通过反复迭代，使得那些适应环境的个体被保存了下来。但相比于进化算法，DE保留了基于种群的全局搜索策略，采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性。同时，DE特有的记忆能力使其可以动态跟踪当前的搜索情况，以调整其搜索策略，具有较强的全局收敛能力和鲁棒性，且不需要借助问题的特征信息，适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题^[20]。除此以外，当然还有其他的还有很多全局优化的技术提出例如NSGA2算法^[8]、基于PSO的NSPSO与CMDPSO^[21],上述两种PSO算法利用了非支配排序、拥挤距离选择、变异算子来提高PSO算法的全局搜索技术。

对于计算时间消耗巨大的问题，也有很多算法来解决。如利用分治思想的有基于分解的多目标进化算法^[22]（MOEA/D）, 这是由张青富等人于2007年提出。MOEA/D将一个多目标优化问题转换为多个标量子问题，且每一个子问题由一个均匀分布的权重向量构成，对于每生成一个新解，则基于聚合函数对该子问题附近的解进行替换。

另外，还有许多研究工作者采用合作协同进化算法（Cooperative Coevolution）与基于代理模型的进化算法来提高进化计算的性能。合作协同进化的主要思想是将大规模问题分解为一组组较小的子问题,现有的有CCPSO、MLCC算法^[23,24]。基于代理模型算法的思想是利用一部分的数据来代理评价另外一部分数据或者利用代理模型达到种群近似评价的效果以减少计算消耗，常见的有CPS，SMEA算法^[25,26]。

二、NP难问题

2.1.定义

非确定性多项式（英语：non-deterministic polynomial，缩写：NP）时间复杂性类，包含了可以在多项式时间内，对一个判定性算法问题的实例，一个给定的解是否正确的算法问题^[17]。

NP是计算复杂性理论中最重要的复杂性类之一。它包含复杂性类P，即在多项式时间内可以验证一个算法问题的实例是否有解的算法问题的集合；同时，它也包含NP完全问题，即在NP中“最难”的问题。计算复杂性理论的中心问题，P/NP问题即是判断对任意的NP完全问题，是否有有效的算法，或者NP与P是否相等。NP问题的形式化定义如下。

对于一个语言L，L在NP中，那么存在多项式时间的图灵机，和多项式P使得：

对于NP困难问题（NP-hard problems）,是指这样的一类问题，它们本身的复杂度是多少无所谓（但由后面的论述可知至少是NP），但是只要这个问题找到确定的多项式时间的解，那么我们可以证明出所有的NP问题都一定存在确定的多项式时间的解。

对于NP完全问题（NP-complete problems）,如果一个问题既是NP困难问题又是NP问题，我们称之为NP完全问题。

NP问题排在世界七大数学难题之首，七个问题都是经过美国克雷数学研究所的科学顾问委员会精心挑选出来的，对这些问题的求解，将会对数学理论的发展与应用产生巨大的推动作用。

2.2 常见的NP难题

2.2.1 哈密顿回路问题

哈密顿回路问题是由天文学家哈密顿(William Rowan Hamilton) 提出，在一个有多个城市的地图网络中， 寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径^[13]。这个问题和著名的过桥问题的不同之处在于，某些城市之间的旅行不一定是双向的。比如A→B,但B→A是不允许的。具体地说，对于一个给定的网络，确定起点和终点后，如果存在一条路径，穿过这个网络，我们就说这个网络存在哈密顿路径。哈密顿路径问题在上世纪七十年代初，终于被证明是“NP完备”的。据说具有这样性质的问题，难于找到一个有效的算法。实际上对于某些顶点数不到100的网络，利用现有最好的算法和计算机也需要很长的时间（可能要几百年之久）才能确定其是否存在一条这样的路径。

2.2.2 旅行商问题

TSP问题（Traveling Salesman Problem）是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路经的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。

求解TSP问题现有很多可行的方法，包括近似算法、概率算法与并行计算。在近似算法中，给定一个最小化问题和一个近似算法，我们按照如下方法评价算法：首先给出最优解的一个下界，然后把算法的运行结果与这个下界进行比较。对于最大化问题，先给出一个上界然后把算法的运行结果与这个上界比较。近似算法比较经典的问题包括：最小顶点覆盖、旅行售货员问题、集合覆盖等。对于概率算法，允许算法在执行的过程中随机选择下一个计算步骤。许多情况下，当算法在执行过程中面临一个选择时，随机性选择常比最优选择省时。因此概率算法可在很大程度上降低算法的复杂度。一般情况下，可将概率算法大致分为四类:数值概率算法，蒙特卡罗（Monte Carlo）算法，拉斯维加斯（Las Vegas）算法和舍伍德（Sherwood）算法^[14]。最后，并行计算或称平行计算是相对于串行计算来说的。所谓并行计算可分为时间上的并行和空间上的并行，极大地减少了搜索的时间。

2.2.3 特征选择问题

在特征选择的发展过程中，出现了三种方法，它们分别是包裹式特征选择（wrapper）、过滤式特征选择（filter）和嵌入式（embedded）方法^[15]。

包裹式特征选择作为一种搜索寻优算法使用分类算法及其性能来选择特征子集。过滤式特征选择使用数据集上的统计或概率学特性来决定选择的特征，如采用信息论中的信息增益或对称不确定性^[29]，此种方法由于不需要采用分类器或学习系统使得它的计算花费较少，但是它的计算准确率不高。嵌入式方法可以在既定模型下学习出能够提高模型准确性较好的特征。由于包裹式特征选择能够获得更加优良的特征子集^[15,16]，本文主要关注包裹式特征选择方法。

现有两种不同类型的包裹式特征选择算法，一种是传统的特征选择算法，如SFS（序列前向选择）和SBS（序列后向选择），这两种都属于贪心算法，SFS的特征子集从空集开始，每次选择一个特征加入特征子集，使得适应度函数最优，SBS则是每次选择一个特征去除。这两种特征选择算法都非常容易陷入局部最优。另一种是基于进化计算的特征选择算法，常见的有遗传算法（GA）,遗传编程（GP）还有基于群体智能的算法，如粒子群算法和蚁群算法等。近年来，由于不同的种群变异策略^[10,11,12]及特征交互分组策略的引入，基于进化计算的包裹式特征选择算法在分类准确度和特征数上优化的效果会更好。

三、基于进化计算的NP难题求解

本节将会具体讨论现有的进化算法在求解NP难问题上的具体方法与策略。由于很多NP问题可以看做一个组合优化问题，因此下文以TSP问题与特征选择问题为例深入。

3.1 TSP问题求解

TSP问题是一个组合优化问题。该问题可以被证明具有NP计算复杂性，迄今为止，这类问题中没有一个找到有效解决算法，因此我们经常用一些近似求解算法，遗传算法、蚁群算法、粒子群算法等。

对于遗传算法求解TSP算法，需要经历编码、初始化、选择、交叉、变异几个步骤。一般来说，针对TSP问题在交叉变异上的特殊性，要采用基于符号编码，我们直接使用路径来表示一个染色体。即使用一个整数数组，数组长度为TSP城市的数量，数组中存储各个城市编号，从下标为0开始逐个遍历数组元素形成的一个序列即为路径(对于要回到原点的要求，为了方便表示，在这里不作考虑，只是在计算路径长度的时候会添加相应的长度)。

如果使用蚁群算法（ACO）来解决TSP问题，需要注意每只蚂蚁带有禁忌表(Tabu)存储已访问过的城市，允许访问的城市表(Allowed)存储还可以访问的城市，矩阵（Delta）来存储它在一个循环迭代中给所经过的路径释放的信息素，除此以外还需要有状态转移概率。在搜索过程中，蚂蚁根据各条路径上的信息量及路径的启发信息来计算状态转移概率。

当然，如果TSP问题中城市的数量较多时，会很容易陷入局部最优，因此需要使用有效的全局搜索技术。具体的TSP问题求解的结果将会在实验中展示。

3.2 特征选择问题求解

在上文2.2.3中介绍到，特征选择除filter和embedded方法外，Wrapper方法更适合应用进化上来。

当进化算法应用到特征选择时，需要将实数值转化为二进制值，因此需要预设一个阈值来决定哪些特征被选中，0代表该特征未选，1代表该特征被选中。

由于特征选择的两个目标是最大化分类性能与最小化特征子集，因此，基于多目标来优化特征选择问题的算法^[27,28]成为研究重点。其中，基于粒子群方法的有薛冰等人提出来的NSPSO和CMDPSO^[21]。前者算法将NSGA2的非支配排序与拥挤距离选择应用到PSO上来；后者采用了拥挤距离与变异支配的策略。这两个算法是第一次将多目标粒子群算法应用到特征选择上来。实验结果表明，NSPSO与CMDPSO能够在一定程度上提升搜索的效率并且可以很大程度上减少特征子集的大小。

四、实验

在此部分，我们将会分别采用不同的进化算法来解决TSP问题与特征选择问题，来验证进化算法在解决NP问题上的实用性。同时在每种问题的实验中，我们也会对比不同算法的性能。

4.1 TSP问题求解

为了验证进化算法解决TSP的性能，我从MTSPLib ^[30]上选择了多个标准测试集数据集，包括低维100维以下与高维1000维。数据集的基本属性如表1所示。

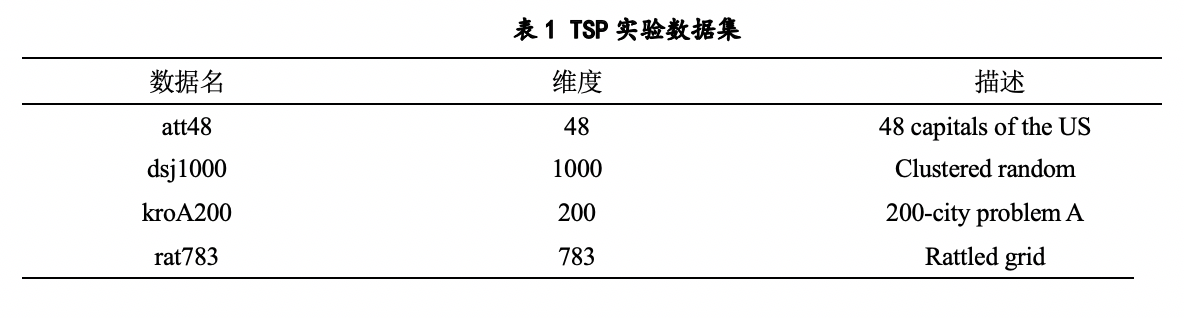
我选取了进化算法中的禁忌搜索算法（TS）、蚁群算法（ACO）、粒子群算法（PSO）及遗传算法（GA）来检查求解TSP问题不同算法的效果。除禁忌搜索算法（TS）与蚁群算法（ACO）是从MTSPLib[30]获取的实验数据外，粒子群算法（PSO）及遗传算法（GA）均进行了10次独立的运行。在PSO算法中，ω=0.7298，c₁=c₂=1.49618，种群大小100；在遗传算法中，交叉概率为0.9，变异概率为0.1，种群大小为100。迭代次数为1000代。所有算法的实验结果如表2所示。

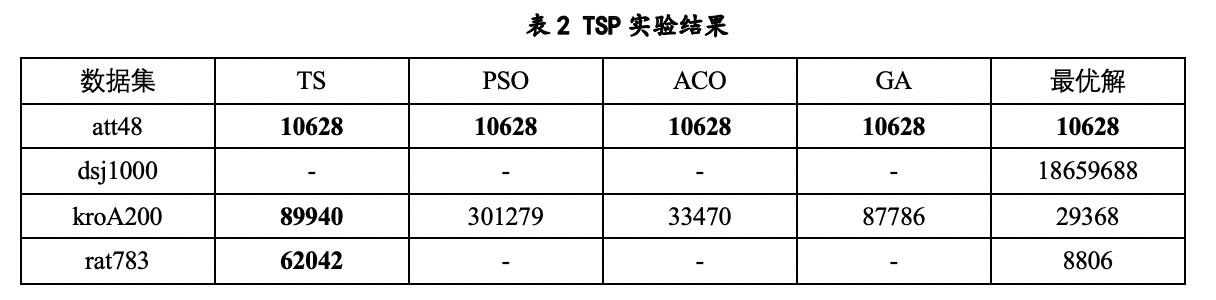
从实验中的结果可以看到，传统的进化算法在解决低维问题，如att48这个数据集上，可以取得很好的效果，4个算法均获得了最优解。对于高维问题如，dsj1000大多数算法在有限的评价次数小不能取得很好的效果。相对于传统算法，禁忌搜索能够取得较优的效果，当然，也有很多研究这对其他算法采取了相应的策略，取得了很好的效果。

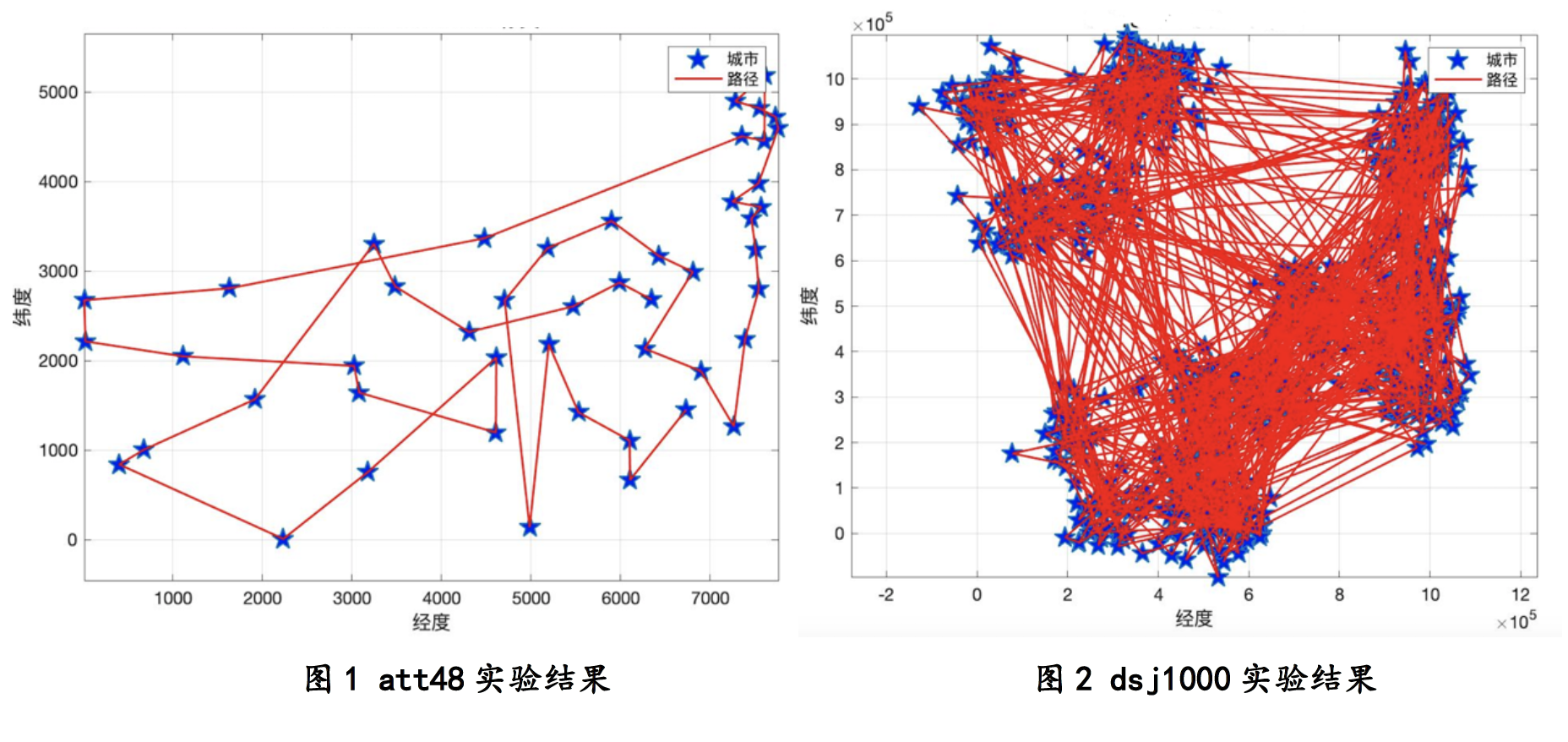
  att48问题最终的结果数据可视化如图1所示，dsj1000高维问题的迭代1000次后的结果如图二所示，可以看到，对于高维问题，需要有相应的策略来避免算法陷入局部最优。

4.2特征选择问题求解

为了验证进化算法解决NP问题特征选择的性能，我从UCI Machine Learning Repository^[30]上选择了多个数据集，数据集的基本属性如表3所示。

表4 特征选择对比算法结果

数据名	算法名称	选出平均特征数	训练集准确率	测试集平均准确率
Wine	SOCSO	8.0	99.12	95.24
	NSPSO	2.4	79.80	79.73
	CMDPSO	3.1	85.88	87.38
	NSGA2	4.4	91.29	91.09
Sonar	SOCSO	31.6	94.84	87.60
	NSPSO	7.2	85.97	71.29
	CMDPSO	15.2	91.07	78.96
	NSGA2	20.0	87.54	80.44
Ionosphere	SOCSO	12.2	94.21	48.57
	NSPSO	3.4	86.51	65.71
	CMDPSO	5.3	91.47	62.86
	NSGA2	10.3	90.53	65.71
Parkinson	SOCSO	13.0	99.85	92.66
	NSPSO	3.5	89.20	83.93
	CMDPSO	4.6	92.97	90.36
	NSGA2	6.6	93.65	89.47
Dermatology	SOCSO	22.0	98.01	94.49
	NSPSO	6.2	86.79	76.41
	CMDPSO	8.8	93.09	92.84
	NSGA2	12.3	93.19	88.95
Spectf	SOCSO	19.4	83.54	73.97
	NSPSO	3.1	81.08	73.07
	CMDPSO	7.3	79.98	73.93
	NSGA2	15.3	77.78	72.33

首先我选取了三个多目标算法，分别是NSGA2算法、NSPSO算法与CMDPSO算法;另外选取了单目标SOCSO^[31]特征选择算法。

实验中，我们在每个数据集上进行了10次独立的运行，在每次独立运行之前，我将数据集随机分成十折，每次选取90%作为训练数据，10%为测试数据，每次运行每一折均使用并在结果去平均值，也就是说算法在某个数据集上，我们一共运行了100次（10次*10折）。训练时，采用的分类器为基于留一法的KNN算法（LOOCV）^[32]，为了能够快速获得数据，我们针对留一法的KNN进行了优化，在迭代之前，实现对数据集中的实例进行了距离计算，并建立了索引，在评价过程中调用索引，大大减少了算法运行时间。KNN算法中K取值为1。在NSPSO中ω=0.7298，c₁=c₂=1.49618；CMDPSO中，ω是0.1至0.5之间的一个随机数，c₁和c₂是1.5至2.0之间的一个随机数；MOCSOFS中的引导向量每隔3代或Pareto前沿面未改进则重新生成；在SOCSO中的c₁与c₂值与NSPSO的相同。在所有的算法中变异概率为1/d,d是种群的维度；实数编码转二进制编码的阈值为0.5。

我从实验结果中选取了平均特征数、训练集准确率、测试集最优准确率和测试集平均准确率四个数据对多个算法进行了对比分析，实验数据结果如表4所示。

从实验结果可以看出，进化算法在解决特征选择分类问题上的准确率已经很高了。因此作为一种组合优化的问题，使用进化算法来解决是很有潜力的。从表4中可以看出单目标特征选择算法在分类精度上较高，但是特征数选出较多，而多目标特征选择算法能够很好地平衡特征数与分类精度。

五、结论

进化算法在很多领域都有广泛的应用，在求解NP问题方面，具有很好的实用性。但是，很多NP问题中，不同的维度之间的交互关联的信息是可以度量的。因此，进化算法不能单纯的随机优化，除启发式函数外，还应该从机器学习的其他方向借鉴不同的思想，有指导性的优化。只有这样，求解NP问题才有更好的延展性，效果才能变得更好。

参考文献

[1] Eiben A E, Schoenauer M. Evolutionary computing[J]. Information Processing Letters, 2002, 82(1): 1-6.

[2] L.J. Fogel, A.J. Owens, M.J. Walsh, Artificial Intelligence through Simulated Evolution, John Wiley, New York, 1966.

[3] Whitley D. A genetic algorithm tutorial[J]. Statistics and computing, 1994, 4(2): 65-85.

[4] Altenberg L. The evolution of evolvability in genetic programming[J]. Advances in genetic programming, 1994, 3: 47-74.

[5] Eberhart R, Kennedy J. A new optimizer using particle swarm theory[C]//Micro Machine and Human Science, 1995. MHS'95., Proceedings of the Sixth International Symposium on. IEEE, 1995: 39-43.

[6] Dorigo M, Birattari M. Ant colony optimization[M]//Encyclopedia of machine learning. Springer, Boston, MA, 2011: 36-39.

[7] Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied soft computing, 2008, 8(1): 687-697.

[8] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.

[9] Mayr E. Behavior Programs and Evolutionary Strategies: Natural selection sometimes favors a genetically" closed" behavior program, sometimes an" open" one[J]. American scientist, 1974, 62(6): 650-659.

[10] Ghamisi P, Benediktsson J A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 309-313.

[11] Tran B, Xue B, Zhang M. A New Representation in PSO for Discretization-Based Feature Selection.[J]. IEEE Transactions on Cybernetics, 2017, PP(99):1-14.

[12] Xue B, Zhang M, Browne W N. Particle swarm optimization for feature selection in classification: a multi-objective approach[J]. IEEE Transactions on Cybernetics, 2013, 43(6):1656-1671.

[13] 赵禹骅, 任伟民, 李可柏. 关于汉密尔顿最短路径的算法[J]. 东方电气评论, 2004, 18(1):42-46.

[14] Hastings W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1):97-109.

[15] 毛勇, 周晓波, 夏铮,等. 特征选择算法研究综述[J]. 模式识别与人工智能, 2007, 20(2):211-218.

[16] Xue B, Zhang M, Browne W N. Particle swarm optimization for feature selection in classification: a multi-objective approach[J]. IEEE Transactions on Cybernetics, 2013, 43(6):1656-1671.

[17] Hochbaum D S. Approximation algorithms for NP-hard problems[M]. PWS Publishing Co., 1996.

[18] Ghaddar B , Naoum-Sawaya J . High Dimensional Data Classification and Feature Selection using Support Vector Machines[J]. European Journal of Operational Research, 2017:S0377221717307713.

[19] Das S, Suganthan P N. Differential Evolution: A Survey of the State-of-the-Art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1):4-31.

[20] Storn R. Differential evolution design of an IIR-filter[C]// IEEE International Conference on Evolutionary Computation. 1996.

[21] Xue B, Zhang M, Browne W N. Particle swarm optimization for feature selection in classification: a multi-objective approach[J]. IEEE Trans Cybern, 2013, 43(6):1656-1671.

[22] Zhang Q, Li H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731.

[23] Yang, K. Tang, and X. Yao, “Multilevel cooperative coevolution for large scale optimization,” in Proc. IEEE Congr. Evol. Comput., Jun. 2008, pp. 1663–1670.

[24] N. Omidvar, X. Li, Z. Yang, and X. Yao, “Cooperative coevolution for large scale optimization through more frequent random grouping,” in Proc. IEEE Congr. Evol. Comput., Jul. 2010,1754–1761.

[25] Liu B, Zhang Q, Gielen G. A Surrogate-Model-Assisted Evolutionary Algorithm for Computationally Expensive Design Optimization Problems with Inequality Constraints[M]// Simulation-Driven Modeling and Optimization. 2016.

[26] Zhang J, Zhou A, Tang K, et al. Preselection via classification: A case study on evolutionary multiobjective optimization[J]. Information Sciences, 2018, 465: 388-403.

[27] Chandrashekar G, Sahin F. A survey on feature selection methods[J]. Computers & Electrical Engineering, 2014, 40(1): 16-28.

[28] Zhang X, Zheng X, Cheng R, et al. A competitive mechanism based multi-objective particle swarm optimizer with fast convergence[J]. Information Sciences, 2018, 427: 63-76.

[29] Lee C, Lee G G. Information gain and divergence-based feature selection for machine learning-based text categorization[M]. Pergamon Press, Inc. 2006.

[30] Lichman M. UCI machine learning repository [Online], avail-able: http://archive.ics.uci.edu/ml, November 10, 2015.

[31] Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization[J]. IEEE transactions on cybernetics, 2015, 45(2): 191-204.

[32] Kearns M, Ron D. Algorithmic stability and sanity-check bounds for leave-one-out cross-validation[J]. Neural computation, 1999, 11(6): 1427-1453.

[33] TSPLib [Online],http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/, 2018