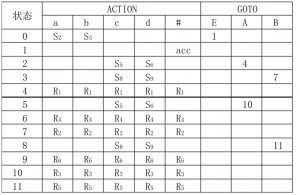
文法简介
1.0型文法(短语文法)
如果对于某文法G,P中的每个规则具有下列形式:
u:: = v
其中u∈V+,v∈V*,则称该文法G为0型文法或短语文法,简写为PSG。
0型文法或短语结构文法的相应语言称为0型语言或短语结构语言L0。这种文法由于没有其他任何限制,因此0型文法也称为无限制文法,其相应的语言称为无限制性语言。任何0型语言都是递归可枚举的,故0型语言又称递归可枚举集。这种语言可由图灵机(Turning)来识别。
2.1型文法(上下文有关文法)
如果对于某文法G,P中的每个规则具有下列形式:
xUy:: = xuy
其中U∈VN;u∈V+;x,y∈V*,则称该文法G为1型文法或上下文有关文法,也称上下文敏感文法,简写为CSG。
1型文法的规则左部的U和右部的u具有相同的上文x和下文y,利用该规则进行推导时,要用u替换U,必须在前面有x和后面有y的情况下才能进行,显示了上下文有关的特性。
1型文法所确定的语言为1型语言L1,1型语言可由线性有界自动机来识别。
3.2型文法(上下文无关文法)
如果对于某文法G,P中的每个规则具有下列形式:
U :: = u
其中U∈VN;u∈V+,则称该文法G为2型文法或上下文无关文法,简写为CFG。
按照这条规则,对于上下文无关文法,利用该规则进行推导时,无需考虑非终结符U所在的上下文,总能用u替换U,或者将u归约为U,显示了上下文无关的特点。
2型文法所确定的语言为2型语言L2,2型语言可由非确定的下推自动机来识别。
一般定义程序设计语言的文法是上下文无关的。如C语言便是如此。因此,上下文无关文法及相应语言引起了人们较大的兴趣与重视。
4.3型文法(正则文法,线性文法)
如果对于某文法G,P中的每个规则具有下列形式:
U :: = T 或 U :: = WT
其中T∈VT;U,W∈VN,则称该文法G为左线性文法。
如果对于某文法G,P中的每个规则具有下列形式:
U :: = T 或 U :: = TW
其中T∈VT;U, W∈VN,则称该文法G为右线性文法。
左线性文法和右线性文法通称为3型文法或正则文法,有时又称为有穷状态文法,简写为RG。
按照定义,对于正则文法应用规则时,单个非终结符号只能被替换为单个终结符号,或被替换为单个非终结符号加上单个终结符号,或者被替换为单个终结符号加上单个非终结符号。
3型文法所确定的语言为3型语言L3,3型语言可由确定的有限状态自动机来识别。
在常见的程序设计语言中,多数与词法有关的文法属于3型文法。
可以看出,上述4类文法,从0型到3型,产生式限制越来越强,其后一类都是前一类的子集,而描述语言的功能越来越弱,四类文法及其表示的语言之间的关系可表示为:
0型 1型 2型 3型;即L0 L1 L2 L3
流程图
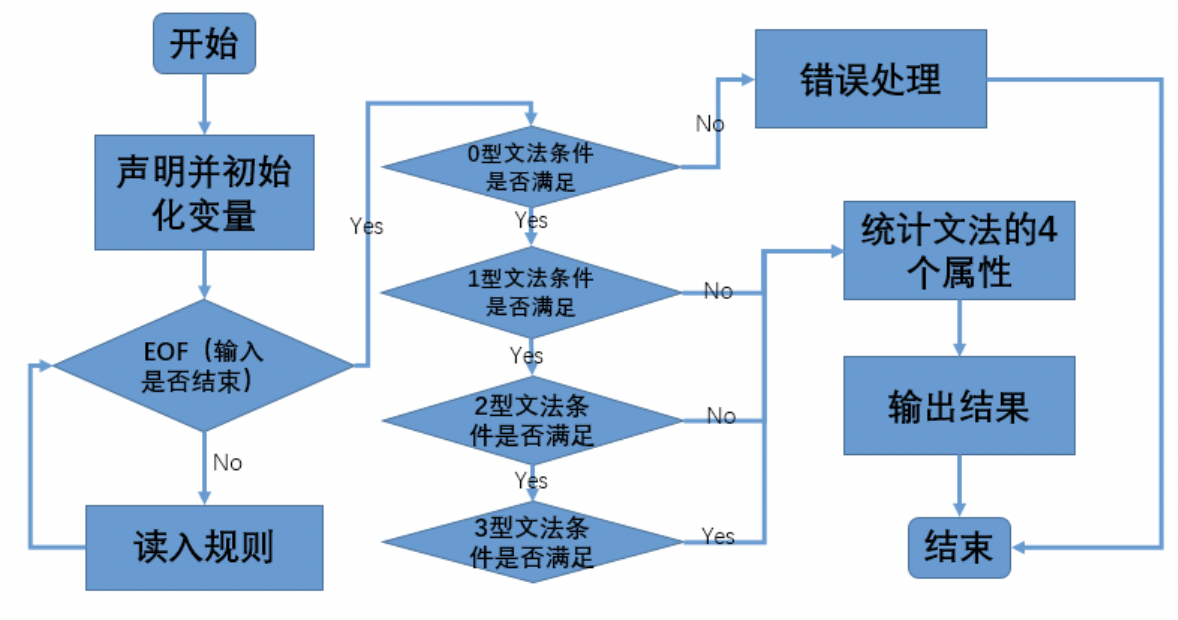
代码
文法的数据结构:考虑到文法是一个四元组,包含Vn为非终结符,Vt为终结符,P为文法的规则,S为识别符或开始符,flag为文法的类型,因此下面使用C++中的类来为文法定义,并且使用set集合来保存每个文法的某些属性(不会重复)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
#include<cstdio> #include<iostream> #include<string> #include<vector> #include<set> #define MAX_LENGTH 10 using namespace std; struct Principle{ string left; string right; }; struct Grammar{ set<char> Vn; set<char> Vt; vector<Principle> P; char S; int flag = -1; }; void input(vector<Principle> &principleSet) { char tempLeft[MAX_LENGTH]; char tempRight[MAX_LENGTH]; while(scanf("%[^-]->%s",tempLeft,tempRight)!=EOF){ getchar(); Principle temp; temp.left = tempLeft; temp.right = tempRight; principleSet.push_back(temp); } } void analyseGram(Grammar &G) { G.S = G.P.front().left[0];//获得起始符 for(int i=0;i<G.P.size();++i){ Principle &temp = G.P[i]; for(int j = 0;j<temp.left.size();++j){ char v = temp.left[j]; if(!isupper(v)){ G.Vt.insert(v); }else{ G.Vn.insert(v); } } for(int j = 0;j<temp.right.size();++j){ char v = temp.right[j]; if(!isupper(v)){ G.Vt.insert(v); }else{ G.Vn.insert(v); } } } } bool existVNT(string s) { for(int i=0;i<s.size();i++){ if(isupper(s[i])){ return true; } } return false; } void judgeGram(Grammar &G) { for(int i=0;i<G.P.size();++i){ if(existVNT(G.P[i].left)){ G.flag = 0; break; } } int temp = 0; for(int i=0;i<G.P.size()&&G.flag==0;++i){ if(G.P[i].left.size()<=G.P[i].right.size()){ temp++; } } if(temp==G.P.size()){ G.flag=1; } temp = 0; for(int i=0;i<G.P.size()&&G.flag==1;++i){ if(1==G.P[i].left.size()&&isupper(G.P[i].left[0])){ temp++; } } if(temp==G.P.size()){ G.flag=2; } temp = 0; for(int i=0;i<G.P.size()&&G.flag==2;++i){ if(1==G.P[i].left.size()&&isupper(G.P[i].left[0])&& (1==G.P[i].right.size()&&!isupper(G.P[i].right[0])|| 2==G.P[i].right.size()&&!isupper(G.P[i].right[0])&& isupper(G.P[i].right[G.P[i].right.size()-1]))){temp++;} } if(temp==G.P.size()){ G.flag=3; } } void printResult(Grammar &G) { cout<<"G=(Vn,Vt,P,S)是"<<G.flag<<"型文法"<<endl<<endl; cout<<"非终结符Vn有:"; for(set<char>::iterator i = G.Vn.begin();i!=G.Vn.end();++i){ cout<<*i<<" "; } cout<<endl; cout<<"终结符Vt有:"; for(set<char>::iterator i = G.Vt.begin();i!=G.Vt.end();++i){ cout<<*i<<" "; } cout<<endl; cout<<"开始符为:"<<G.S<<endl; cout<<"规则P如输入所示"<<endl; cout<<endl; } int main() { Grammar G; G.Vn.clear(); G.Vt.clear(); input(G.P); G.flag = 3; analyseGram(G); judgeGram(G); printResult(G); } |
实验验证
1型文法实验结果

2型文法实验结果
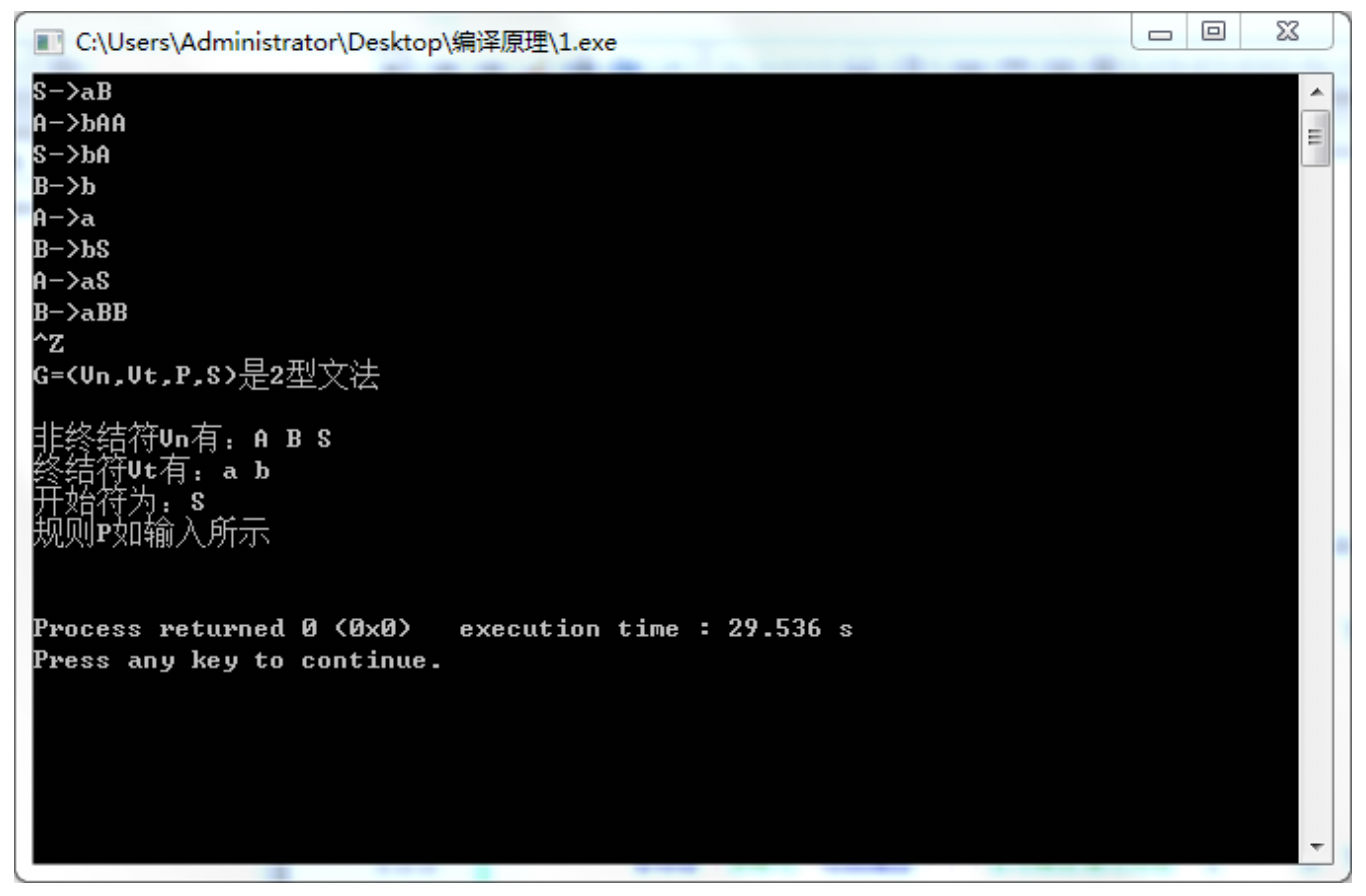
3型文法实验结果
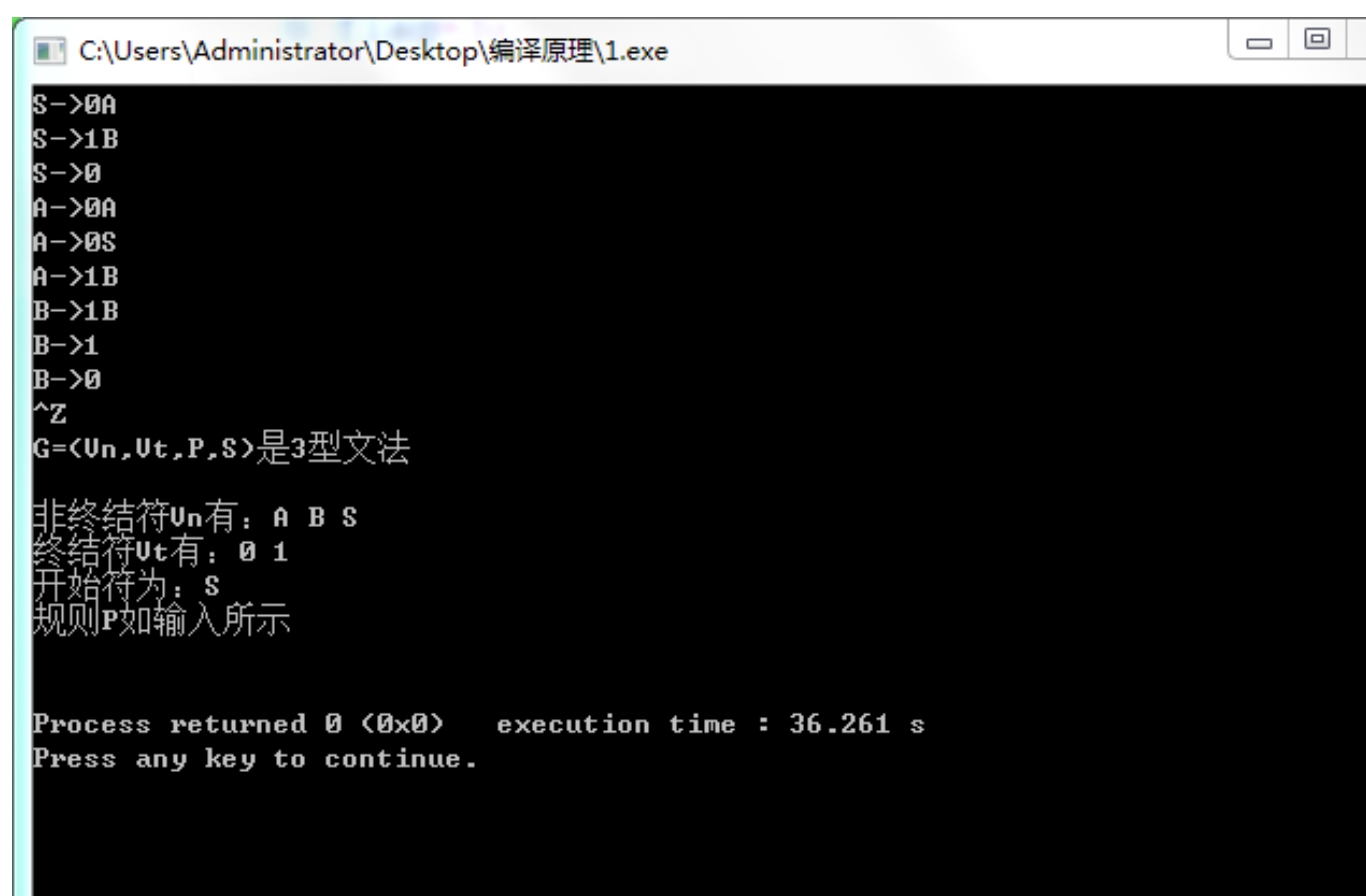
困难与解决方法
- 数据结构的建立
为了便于以后实验的代码复用,需要建立一个良好的数据结构类型。因此本次实验我采用了C++来写,并使用了C++中的容器,如set和vector。
- 文法类型的判断方式
这一部分是此次实验的重点,如何有效地判断文法的类型是一个难题。经过分析后,我决定自上而下,由低到高地来判断文法的类型。首先判断是否为低级文法,再判断是否为高级文法。在判断过程中出现很多分支语句,因此可以将某些模块提出,比如非终结符判断模块,可以整合为函数bool existVNT(string s)。
- 如果一开始实验中输入的格式不对,对此种问题我们可以有两种解决方法,一种是在输入的时候立即判断是否是合法的规则,也可以在文法类型判断是输出错误消息。