文章目录
二叉树
二叉树是一种每个结点至多只有两个子树(即二叉树的每个结点的度不大于2),并且二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的性质
- 在二叉树的第i层,至多有2^(i-1)个结点
- 深度为k的二叉树至多有:(2^k)-1个结点,其实这个结果就是一个等比数列的求和得到的。
- 对任意一颗二叉树,如果其叶子结点数量为:n0,度为2的结点数为:n2,则:n0=n2+1
二叉树的数据结构
C++实现二叉树时,有很多数据结构,具体采用哪种数据结构,需要根据问题具体选择。
常见的有
- 数组存储:此种存储方式一般是按照前序后序或中序输入,求出另一种遍历的输出
- 链表存储,链表存储一般采用struct结构,具体如下,l, r分别是当前节点左孩子和右孩子的id值
|
1 |
struct node{int l, r;}a[100]; |
当然也可以采用纯链表的方式,采用纯链表的方式可以递归构造二叉树
|
1 2 3 4 5 6 7 8 9 |
/结点的结构 struct node{ //每个结点的数据 int data; //左子树 Tree_Node * left; //右孩子 Tree_Node * right; }; |
实例
前序后序遍历
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
#include <iostream> using namespace std; void ToPost(char *inOrder, char *preOrder, int length){ if(length<=0)return; int root; for(root=0;root<length;root++){ if(inOrder[root]==preOrder[0])break; } ToPost(inOrder,preOrder+1,root); ToPost(inOrder+root+1,preOrder+root+1,length-root-1); cout<<preOrder[0]; } void ToPre(char *inOrder, char *postOrder, int length){ if(length<=0)return; int root; for(root=0;root<length;root++){ if(inOrder[root]==postOrder[length-1])break; } cout<<postOrder[length-1]; ToPre(inOrder,postOrder,root); ToPre(inOrder+root+1,postOrder+root,length-root-1); } int main() { char pre[]="ABDECFG"; char in[]="DBEAFCG"; char post[]="DEBFGCA"; cout<<"原始序列:\n"; cout<<"Pre:"<<pre<<endl <<"In:"<<in<<endl <<"Post:"<<post<<endl; cout<<"后序遍历:\n"; ToPost(in,pre,8); cout<<endl; cout<<"前序遍历:\n"; ToPre(in,post,8); cout<<endl; return 0; } |
PAT 1115 Counting Nodes in a BST (30 分)
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Insert a sequence of numbers into an initially empty binary search tree. Then you are supposed to count the total number of nodes in the lowest 2 levels of the resulting tree.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer () which is the size of the input sequence. Then given in the next line are the integers in which are supposed to be inserted into an initially empty binary search tree.
Output Specification
For each case, print in one line the numbers of nodes in the lowest 2 levels of the resulting tree in the format:
|
1 2 |
n1 + n2 = n |
where n1 is the number of nodes in the lowest level, n2 is that of the level above, and n is the sum.
Sample Input
|
1 2 3 |
9 25 30 42 16 20 20 35 -5 28 |
Sample Output
|
1 |
2 + 4 = 6 |
C++代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
#include<iostream> #include<vector> using namespace std; struct node { int v; struct node *left, *right; }; node* build(node *root, int v){ if(root == NULL){ root = new node(); root->v = v; root->left = root->right = NULL; }else if(v <= root->v) root->left = build(root->left, v); else root->right = build(root->right, v); return root; } vector<int> num(1000); int maxDepth = -1; void dfs(node *root, int depth){ if(root == NULL){ maxDepth = max(depth, maxDepth); return; } num[depth]++; dfs(root->left, depth + 1); dfs(root->right, depth + 1); } int main(){ int n; cin>>n; node *root = NULL; for(int i = 0; i < n; i++){ int t; cin>>t; root = build(root, t); } dfs(root, 0); printf("%d + %d = %d\n", num[maxDepth - 1], num[maxDepth - 2], num[maxDepth - 1] + num[maxDepth - 2]); return 0; } |
PAT 1135 Is It A Red-Black Tree
There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:
- (1) Every node is either red or black.
- (2) The root is black.
- (3) Every leaf (NULL) is black.
- (4) If a node is red, then both its children are black.
- (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.
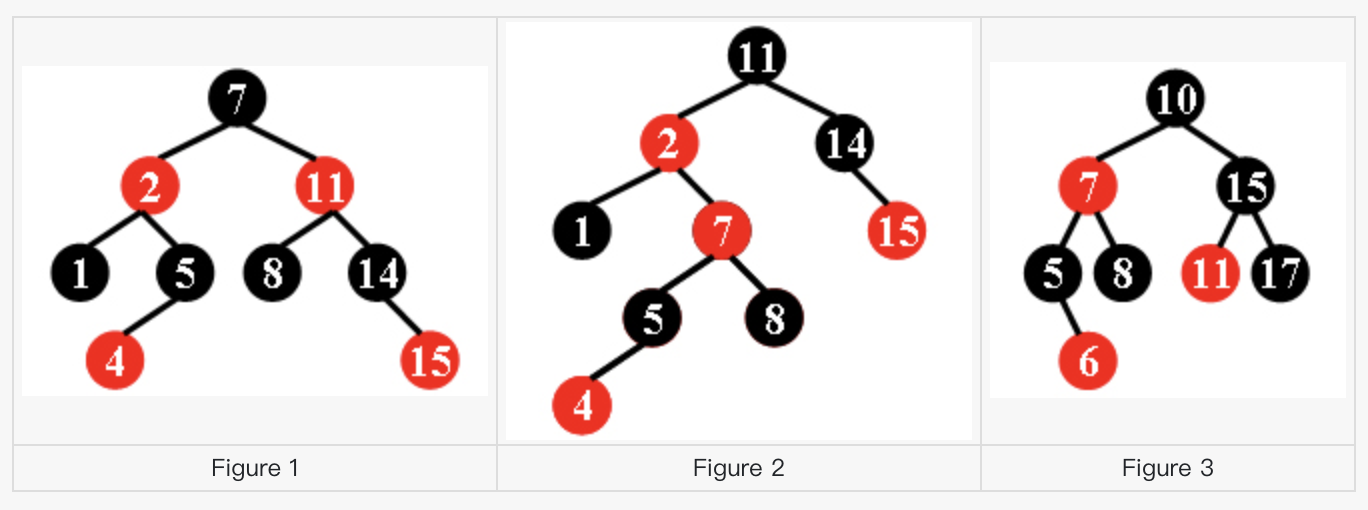
For each given binary search tree, you are supposed to tell if it is a legal red-black tree.
Input Specification
Each input file contains several test cases. The first line gives a positive integer K (30) which is the total number of cases. For each case, the first line gives a positive integer N (30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.
Output Specification
For each test case, print in a line “Yes” if the given tree is a red-black tree, or “No” if not.
Sample Input
|
1 2 3 4 5 6 7 8 |
3 9 7 -2 1 5 -4 -11 8 14 -15 9 11 -2 1 -7 5 -4 8 14 -15 8 10 -7 5 -6 8 15 -11 17 |
Sample Output
|
1 2 3 |
Yes No No |
C++代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include<iostream> #include<vector> #include<cmath> using namespace std; vector<int> arr; struct node{ int val; struct node *left, *right;//以链表的方式存储 }; node* build(node *root, int v){ //递归二叉查找树 if(root == NULL){ root = new node(); root->val = v; root->left = root->right = NULL; }else if(abs(v) <= abs(root->val))//小于根节点的为左边递归 root->left = build(root->left, v); else root->right = build(root->right, v); return root; } bool judgeBlackChild(node *root){ //判断红色节点的孩子为黑色 if(root == NULL)return true; if(root->val < 0){//red negative if(root->left != NULL && root->left->val < 0 )return false; if(root->right != NULL && root->right->val < 0)return false; } return judgeBlackChild(root->left) && judgeBlackChild(root->right); } int getNum(node *root){ if(root == NULL)return 0; int l = getNum(root->left); int r = getNum(root->right); return root->val > 0 ? max(l, r) + 1 : max(l, r); //大于0是黑色节点,如果是黑色节点则加1,否则不变 } int judgeBlackNum(node *root){ //判断数量是否相同 if(root == NULL)return true; int l = getNum(root->left); int r = getNum(root->right); if(l != r)return false; return judgeBlackNum(root->left) && judgeBlackNum(root->right); } int main(){ int k, n; cin>>k; for(int i = 0; i < k; i++){ cin>>n; arr.resize(n); node *root = NULL; for(int j = 0; j < n; j++){ cin>>arr[j]; root = build(root, arr[j]); } if(arr[0] < 0 || !judgeBlackChild(root)|| !judgeBlackNum(root)) cout<<"No\n"; else cout<<"Yes\n"; } return 0; } |
PAT 1110 Complete Binary Tree (25 分)
Given a tree, you are supposed to tell if it is a complete binary tree.
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer () which is the total number of nodes in the tree — and hence the nodes are numbered from 0 to . Then lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a - will be put at the position. Any pair of children are separated by a space.
Output Specification
For each case, print in one line YES and the index of the last node if the tree is a complete binary tree, or NO and the index of the root if not. There must be exactly one space separating the word and the number.
Sample Input 1
|
1 2 3 4 5 6 7 8 9 10 11 |
9 7 8 - - - - - - 0 1 2 3 4 5 - - - - |
Sample Output 1
|
1 2 |
YES 8 |
Sample Input 2
|
1 2 3 4 5 6 7 8 9 10 |
8 - - 4 5 0 6 - - 2 3 - 7 - - - - |
Sample Output 2
|
1 |
NO 1 |
C++代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#include<iostream> #include<vector> using namespace std; struct node{int l, r;}a[100]; int maxn = -1, ans; void dfs(int root, int index){ if(index > maxn){ //找到index最大的点如果maxn == n则ok maxn = index; ans = root; } if(a[root].l != -1) dfs(a[root].l, index * 2); if(a[root].r != -1) dfs(a[root].r, index * 2 + 1); } int main(){ int n, root = 0, have[100] = {0}; cin>>n; for(int i = 0; i < n; i++){ string l, r; cin>>l>>r; if(l == "-"){ a[i].l = -1; }else{ a[i].l = stoi(l); have[stoi(l)] = 1; } if(r == "-"){ a[i].r = -1; }else{ a[i].r = stoi(r); have[stoi(r)] = 1; } } while(have[root] != 0)root++; dfs(root, 1); if(maxn == n)//输出last node cout<<"YES "<<ans<<endl; else//输出根 cout<<"NO "<<root<<endl; return 0; } |
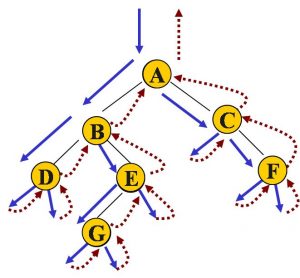
PAT 1102 Invert a Binary Tree (25 分)
The following is from Max Howell @twitter:
|
1 2 |
Google: 90% of our engineers use the software you wrote (Homebrew), but you can't invert a binary tree on a whiteboard so fuck off. |
Now it’s your turn to prove that YOU CAN invert a binary tree!
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer () which is the total number of nodes in the tree — and hence the nodes are numbered from 0 to . Then lines follow, each corresponds to a node from 0 to , and gives the indices of the left and right children of the node. If the child does not exist, a - will be put at the position. Any pair of children are separated by a space.
Output Specification
For each test case, print in the first line the level-order, and then in the second line the in-order traversal sequences of the inverted tree. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input
|
1 2 3 4 5 6 7 8 9 10 |
8 1 - - - 0 - 2 7 - - - - 5 - 4 6 |
Sample Output
|
1 2 |
3 7 2 6 4 0 5 1 6 5 7 4 3 2 0 1 |
C++代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
#include<iostream> #include<vector> #include<algorithm> using namespace std; struct node{int id, l, r, index, level;}a[100]; //id, l, r是输入的值, index是层序的值,level是层数 vector<node> v1; void dfs(int root, int index, int level){ if(a[root].r != -1)dfs(a[root].r, index * 2 + 2, level + 1); node temp; temp.id = root; temp.l = 0; temp.r = 0; temp.index = index; temp.level = level; v1.push_back(temp);//存入中序值 if(a[root].l != -1)dfs(a[root].l, index * 2 + 1, level + 1); } bool cmp(node a, node b){ if(a.level != b.level)return a.level < b.level; //返回层数小的 return a.index > b.index; //倒过来输出,因此层数相同时,先返回大的 } int main(){ int n, root = 0, ext[100]; cin>>n; for(int i = 0; i < n; i++){ string l, r; cin>>l>>r; if(l == "-"){ a[i].l = -1; }else{ a[i].l = stoi(l); ext[stoi(l)] = 1; } if(r == "-"){ a[i].r = -1; }else{ a[i].r = stoi(r); ext[stoi(r)] = 1; } } while(ext[root] != 0)root++; dfs(root, 0, 0); vector<node> v2(v1); sort(v2.begin(), v2.end(), cmp); for(int i = 0; i < v2.size(); i++){//中序 printf("%d%s", v2[i].id, i == v2.size() - 1 ? "\n" : " "); } for(int i = 0; i < v1.size(); i++){//中序 printf("%d%s", v1[i].id, i == v1.size() - 1 ? "\n" : " "); } return 0; } |
PAT 1099 Build A Binary Search Tree (30 分)
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
- Both the left and right subtrees must also be binary search trees.
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.
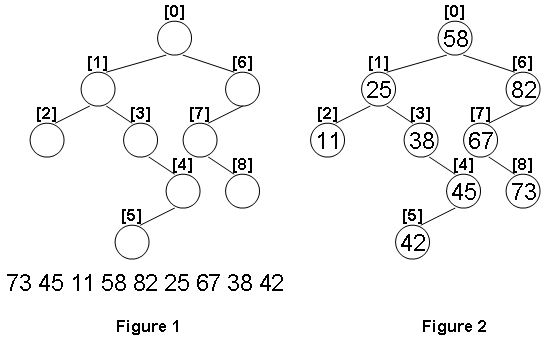
Input Specification
Each input file contains one test case. For each case, the first line gives a positive integer () which is the total number of nodes in the tree. The next lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to , and 0 is always the root. If one child is missing, then will represent the NULL child pointer. Finally distinct integer keys are given in the last line.
Output Specification
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.
Sample Input
|
1 2 3 4 5 6 7 8 9 10 11 12 |
9 1 6 2 3 -1 -1 -1 4 5 -1 -1 -1 7 -1 -1 8 -1 -1 73 45 11 58 82 25 67 38 42 |
Sample Output:
|
1 |
58 25 82 11 38 67 45 73 42 |
C++代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
#include<iostream> #include<algorithm> #include<vector> using namespace std; struct node{ int l, r, index, data, level; }a[100]; //id, l, r是输入的序号,index是排序的序号, level是层数 vector<int> val; int id = 0; void dfs(int root, int index, int level){ //先序遍历 if(a[root].l != -1) dfs(a[root].l, index * 2 + 1, level + 1); a[root].level = level; a[root].index = index; a[root].data = val[id++]; if(a[root].r != -1) dfs(a[root].r, index * 2 + 2, level + 1); } bool cmp(node a, node b){ if(a.level != b.level) return a.level < b.level; return a.index < b.index; } int main(){ int n, root = 0; cin>>n; for(int i = 0; i < n; i++){ int l, r; cin>>a[i].l>>a[i].r; } for(int i = 0; i < n; i++){ int temp; cin>>temp; val.push_back(temp); } sort(val.begin(), val.end()); dfs(root, 0, 0); sort(a, a + n, cmp); for(int i = 0; i < n; i++){ printf("%d%s", a[i].data, i == n - 1 ? "\n" : " "); } return 0; } |