互信息的定义
正式地,两个离散随机变量 X 和 Y 的互信息可以定义为:
其中 p(x,y) 是 X 和 Y 的联合概率分布函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。
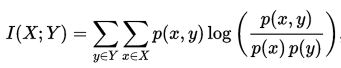
在连续随机变量的情形下,求和被替换成了二重定积分:
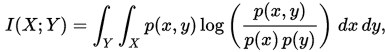
其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。
互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。如果对数以 2 为基底,互信息的单位是bit。
直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y 共享:知道 X 决定 Y 的值,反之亦然。因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的熵。而且,这个互信息与 X 的熵和 Y 的熵相同。(这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。)
互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。于是互信息以下面方式度量依赖性:I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出:当 X 和 Y 独立时,p(x,y) = p(x) p(y),因此:
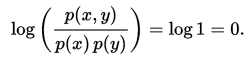
此外,互信息是非负的(即 I(X;Y) ≥ 0; 见下文),而且是对称的(即 I(X;Y) = I(Y;X))。
通用MATLAB代码
主函数main.m
|
1 2 3 4 5 |
clc u1 = rand(4,1); u2 = [2;32;6666;5]; wind_size = size(u1,1); mi = calmi(u1, u2, wind_size); |
calmi.m
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
%计算两列向量之间的互信息 %u1:输入计算的向量1 %u2:输入计算的向量2 %wind_size:向量的长度 function mi = calmi(u1, u2, wind_size) x = [u1, u2]; n = wind_size; [xrow, xcol] = size(x); bin = zeros(xrow,xcol); pmf = zeros(n, 2); for i = 1:2 minx = min(x(:,i)); maxx = max(x(:,i)); binwidth = (maxx - minx) / n; edges = minx + binwidth*(0:n); histcEdges = [-Inf edges(2:end-1) Inf]; [occur,bin(:,i)] = histc(x(:,i),histcEdges,1); %通过直方图方式计算单个向量的直方图分布 pmf(:,i) = occur(1:n)./xrow; end %计算u1和u2的联合概率密度 jointOccur = accumarray(bin,1,[n,n]); %(xi,yi)两个数据同时落入n*n等分方格中的数量即为联合概率密度 jointPmf = jointOccur./xrow; Hx = -(pmf(:,1))'*log2(pmf(:,1)+eps); Hy = -(pmf(:,2))'*log2(pmf(:,2)+eps); Hxy = -(jointPmf(:))'*log2(jointPmf(:)+eps); MI = Hx+Hy-Hxy; mi = MI/sqrt(Hx*Hy); |
互信息概述请跳转至
互信息特征选择请跳转至



MI是求出的互信息,那么mi是什么呢?谢谢
好用,谢谢!