定义:若干冲突或相互影响条件约束下在给定区域内寻找尽可能的最优解(非劣解)。
关键词:条件约束,折中最优解(解并非唯一是与单目标优化问题的本质区别)
文字描述:
D个决策变量参数;
N个目标函数;
m+n个约束条件。
数学描述:
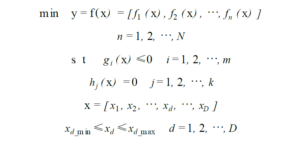
X(小写)为D维决策向量;y为目标向量;N为优化目标总数;gi(x)<=0和hj(x)为条件约束(为已知确定的可行域);X(大写)是决策向量形成的决定空间;Y是目标向量形成的目标空间;xd_max和xd_min是每维向量搜索的上下限。
注释:

下图是多目标优化问题中最优解或非劣最优解的定义

一些关于Pareto最优解的文献解释:
若x*∈C,且在C中不存在比x*更优越的解x,则称x*是多目标最优化模型式的Pareto最优解,又称为有效解。
一般来说,多目标优化问题并不存在一个最优解,所有可能的解都称为非劣解,也称为Pareto解.传统优化技术一般每次能得到Pareto解集中的一个,而用遗传算法来求解,可以得到更多的Pareto解,甚至是整个的解都成为Pareto解
这些解构成了一个最优解集,称为Pareto最优解.它是由那些任一个目标函数值的提高都必须以牺牲其他目标函数值为代价的解组成的集合,称为Pareto最优域,简称Pareto集
多目标规划的基本概念之一.对于包括有定量和定性属性的多指标决策问题(参见“多目标决策问题”),其非劣解是指在所给的可供选择的方案集中,已找不到使每一指标都能改进的解.在多目标规划中,它即指有效解(参见“有效解”)和较多最优解(参见“较多最优解”)。
所谓非劣解是指由这样一些解组成的集合(又称非劣解集):与集合之外的任何解相比它们至少有一个目标函数比集合之外的解好而其它目标函数又不比集合之外的解差。
不同算法在多目标优化中的应用
多目标优化问题不存在唯一的全局最优解。但仍然需要寻找到1个最终解。
有三类方法:
1.生成法:大量求非劣解,从中寻找最优解。
2.交互法:分析目标求出最优解。
3.将多目标问题转换为单目标问题求解。
原创文章非商业转载请注明出处,商业转载请联系。